Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 7
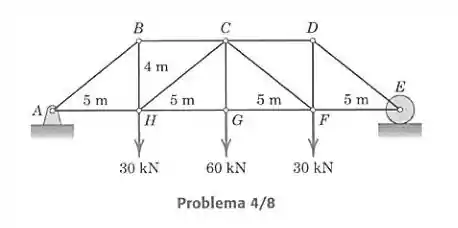
Determine a força em cada elemento da treliça carregada. Utilize a simetria da treliça e do carregamento.
Passo 1
Vamos calcular as forças pelo método dos nós, isolando cada pino da treliça. Primeiro vamos às equações externas da treliça, para acharmos os valores de reação de e . Note que o apoio em só causa reação para cima:
Agora encontramos através da equação do momento em torno de :
Passo 2
Agora vamos calcular as equações para cada nó. indica que a barra está comprimida e indica que ela está tracionada. Se o valor de uma força der negativo significa que erramos o sentido. Pela simetria do problema, observamos as seguintes relações.
Então encontrando metade das forças conseguiremos definir todas.
Passo 3
Nó A:
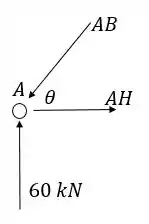
Analisando o triângulo , calculamos o tamanho por Pitágoras:
Então temos o seno e o cosseno do ângulo entre e :
Todos os outros triângulos do problema são semelhantes a esse. Temos para o nó A então:
Pela simetria, temos também:
Passo 4
Nó B:
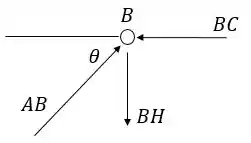
Por simetria, temos também:
Passo 5
Nó H:
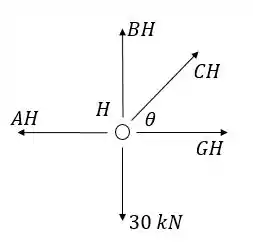
Substituindo o valor de
Substituindo o valor de
O valor negativo indica que é de compressão e não de tração. Agora encontramos :
Por simetria, obtemos também:
Passo 6
Nó G:
Como uma simples soma de forças no eixo , obtemos :