Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 56
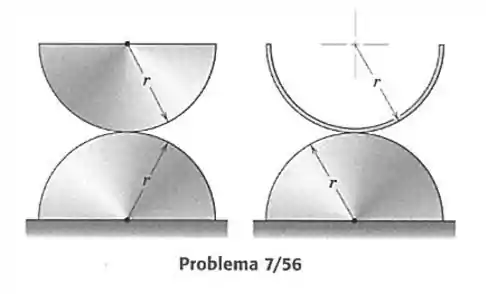
56- Determine por meio de cálculos se o semicilindro homogêneo e a casca semicilíndrica permanecerão nas posições mostradas ou se eles rolarão sobre os cilindros inferiores.
Passo 1
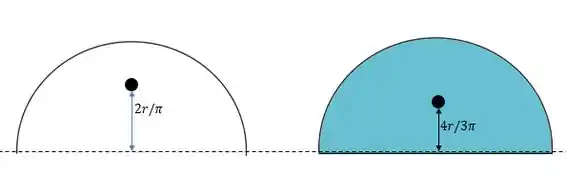
Das disciplinas de cálculo e do capítulo desse livro nós sabemos que o centroide de semicírculo é de:
E de uma casca semicilíndrica é de:
Para saindo do centro desse semicírculo, tal como nas imagens abaixo.
Passo 2
Agora resolvendo o sistema de modo genérico (ou seja entortando o corpo de cima um ângulo no plano) temos a seguinte representação( considerando que o eixo nulo está na base):
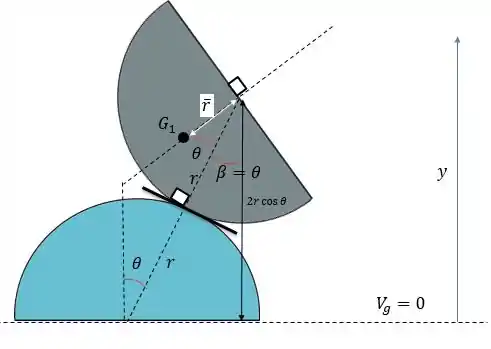
Entendendo o rebatimento de ângulos na figura entende-se tranquilamente o problema todo. Como os dois cilindros tem o mesmo raio pode-se calcular o valor de da seguinte maneira:
Pois é o comprimento do arco feito pelos dois círculos na movimentação do circulo maior (não há nenhum translado).
Logo rebatendo a altura de na vertical temos:
O que dá uma equação de energia potencial gravitacional igual a, considerando que o corpo superior tem massa :
Passo 3
Derivando essa equação em relação a temos:
Derivando de novo temos:
Para temos:
Substituindo os valores de temos:
Para a letra onde
Como é menor que 1 então o sistema na letra é instávell em
Para a letra b onde
Como então a equação é positiva, o que configura em um sistema estável.
Resposta
- Instável
- Estável