Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 65
O dispositivo serve como uma mola de torção compacta. É feito de aço A-36 e composto por um eixo interno maciço embutido em um tubo e acoplado a esse tubo por um anel rígido em . Podemos considerar que o anel em também é rígido e está preso de modo que não pode girar. Se um torque for aplicado ao eixo, determine o ângulo de torção na extremidade e a tensão de cisalhamento máxima no tubo e eixo.
Passo 1
Olá, pessoal! Tudo bem? Vamos analisar essa questão?
O problema pede que determinemos o ângulo de torção na extremidade e a tensão de cisalhamento máxima no tubo e no eixo. E nos fornece como dados:
Aço A-36, portanto,
O eixo maciço e o tubo estão submetidos ao mesmo torque , logo o ângulo de torção na extremidade será a soma do ângulo do segmento e do segmento :
Determinaremos a tensão de cisalhamento máxima no eixo maciço e no tubo, através da equação:
Passo 2
Vamos agora calcular os valores dos torques. Para isso, vamos ilustrar o problema para ter melhor ideia do que queremos.
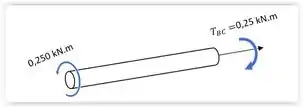
Como podemos observar, o torque é igual ao torque que corre em .
Fica mais fácil imaginar que ao aplicar um torque no tubo , o eixo maciço também vai sofrer o efeito desse torque, tendo uma torção provocada no mesmo sentido. Portanto:
Passo 3
Com os torques determinados nos resta apenas encontrar os momentos polares de inércia e aplicar na fómula do ângulo de torção:
A região é uma haste maciça de diâmetro igual a . Logo,
A região é um tubo de diâmetro externo igual a e raio interno igual a . Então:
Passo 4
O ângulo é dado por:
Sendo que:
Logo:
Convertendo para radianos:
Passo 5
A tensão é dada pela proximidade da prova multiplicada pelo tanto de dias vendo séries. Ou então por:
Já que queremos achar a tensão máxima devemos usar o raio externo no calculo referente a seção tubular. Calculando para cada seção, temos: