Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 66
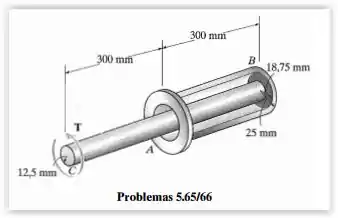
O dispositivo serve como uma mola de torção compacta. É feito de aço A-36 e composto por um eixo interno maciço embutido em um tubo e acoplado a esse tubo por um anel rígido em . Podemos considerar que o anel em também é rígido e está preso de modo que não pode girar. Se a tensão de cisalhamento admissível para o material for e o ângulo de torção em estiver limitado a , determine o torque máximo que pode ser aplicado na extremidade .
Passo 1
Olá, pessoal! Tudo bem? Vamos analisar essa questão?
O problema pede que determinemos um torque máximo admissível que possa ser aplicado a sua extremidade, não ultrapasse e . Nos foi fornecido:
Aço A-36, portanto,
O eixo maciço e o tubo estão submetidos ao mesmo torque , logo o ângulo de torção na extremidade será a soma do ângulo do segmento e do segmento :
Podemos usar essa expressão para calcular , substituindo pelo ângulo de torção admissível. Depois substituiremos o valor obtido na equação da tensão de cisalhamento máxima para verificar se obedece ao estabelecido .
Se obdecer, então esse será o torque máximo, porque qualquer torque acima desse valor vai ultrapassar o ângulo de 3°. Se exceder, calcularemos fazendo o inverso: substituir primeiro na equação da tensão máxima e depois verificar se obedece aos requisitos do ângulo .
Passo 2
Cálculo dos momentos polares de inércia:
A região é uma haste maciça de diâmetro igual a . Logo,
A região é um tubo de diâmetro externo igual a e raio interno igual a . Então:
Passo 3
Com os momentos de inércia já calculados, vamos então encontrar o torque usando o ângulo de torção máximo admissível. Como ele foi fornecido em graus, temos q convertê-lo para radianos:
Substituindo o torque na fórmula da tensão, vamos verificar tanto para o segmento , quanto para o segmento .
Para o segmento :
Para o segmento :
Ambos os resultados foram menores que a tensão admissível. Portanto, o torque máximo é::