Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas de Revisão - Ex. 158

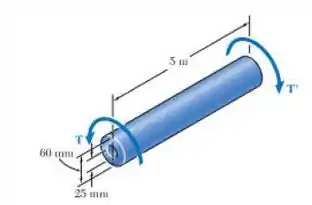
Enquanto o eixo vazado de aço rotaciona a 180 rpm, uma medida estroboscópica indica que o ângulo de torção é igual a 3°. Sabendo que G = 77,2   G P a , determine (a) a potência transmitida e (b) a máxima tensão de cisalhamento do eixo.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a potência transmitida e a máxima tensão de cisalhamento do eixo. Para isso vamos determinar o raio interno e externo antes de mais nada !

c 2 = 1 2 d 2 = 30   m m c 1 = 1 2 d 1 = 12,5   m m

Agora podemos determinar J , venha :D

J = π 2 c 2 4 - c 1 4 = π 2 30 4 - 12,5 4 = 1,234   x   10 6 m m 4 = 1,234   x   10 - 6 m 4

O ângulo é dado por φ = 3 ° = 0,05236   r a d então podemos calcular a torção φ = T L G J T = G J φ L = 77,2   x   10 9   x   1,234   x   10 - 6   x   ( 0,0536 ) 5 = 997,61   m

Passo 2

A Velocidade angular: f = 180   r p m = 3   r e v / s e c = 3 H z então agora podemos determinar a potencia 😉

  1. P = 2 π f T = 2 π   x   3   x   997,61 = 18,80   x   10 3 W

E agora a tensão máxima de cisalhamento

b) τ m = T c 2 J = 997,61   x   30   x   10 - 3 1,234   x   10 - 6 = 24,3   x   10 6 P a

Resposta

  1. P = 18,80   k W
  2. τ m = 24,3   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os dois eixos são feitos de aço A-36. Cada eixo tem diâmetro de 25m m e os dois estão acoplados pelas engrenagens presas a uma das extremidades de cada um deles. As outras extremidades de cada um dos
Uma porção do eixo de aço A-36 é submetida a um carregamento de torção distribuído linearmente. Se o eixo tiver as dimensões mostradas na figura, determine as reações nos apoios fixos A e C . O segmen
O eixo de raio c é submetido a um torque distribuído t , medido como torque/comprimento do eixo. Determine as reações nos apoios A e B.
Determine a rotação da engrenagem em E no Problema 5.81.
O eixo cônico está confinado pelos apoios fixos em A e B . Se for aplicado um torque T em seu ponto médio, determine as reações nos apoios.