Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas de Revisão - Ex. 160
Uma barra de latão tem a seção vazada mostrada na figura. Sabendo que a tensão de cisalhamento não pode exceder 82,7 MPa e desprezando o efeito da concentração de tensões, determine o maior troque possível de ser aplicada ao eixo.
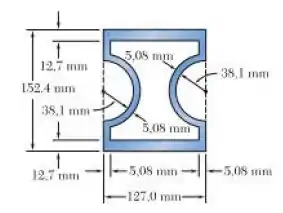
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine o maior troque possível de ser aplicada ao eixo, então vamos esboçar o elemento:
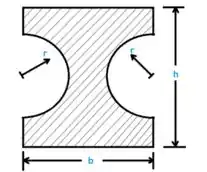
Para calcularmos a área delimitada pela linha central da seção transversal da parede. A área é um retângulo com dois recortes semicirculares.
Assim podemos determinar a área:
Então podemos determinar a tensão de cisalhamento
E o torque é obtido tal qual abaixo:
Resposta
Exercícios de Livros Relacionados
Determine a rotação da junta B e a tensão de cisalhamento máxima absoluta no eixo do Problema 5.85 .
O eixo de aço tem 300m m de comprimento e é parafusado em uma parede com uma chave de torque. Determine as maiores forças conjugadas F que podem ser aplicadas ao eixo sem provocar o escoamento do aço.
O cabo de latão tem seção transversal triangular de 2m m em um lado. Se a tensão de escoamento para o latão for τ e = 205M P a , determine o torque máximo T ao qual o cabo pode ser submetido de modo a
O eixo é feito de plástico e tem seção transversal elíptica. Se for submetido ao carregamento de torção mostrado, determine a tensão de cisalhamento no ponto A e mostre a tensão de cisalhamento em um
O eixo de aço tem 300m m de comprimento e é parafusado em uma parede com uma chave de torque. Determine a máxima tensão de cisalhamento no eixo e o deslocamento que cada força conjugada sofre se o val