Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas de Revisão - Ex. 160

Três placas de aço são soldadas juntas para formar a viga mostrada. Sabendo que a tensão normal admissível para o aço utilizado é de 22 ksi, determine a largura mínima b do flange que poderá ser usada.

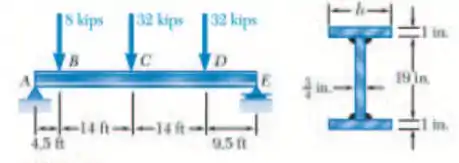
Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a tensão normal admissível para o aço utilizado é de 22 ksi, determine a largura mínima b do flange que poderá ser usada. Para isso vamos começar esboçando o diagrama de corpo livre ;)

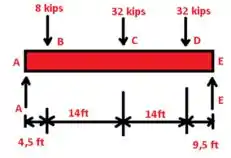
Passo 2

E ai gurizada vamos calcular primeiramente o somatório em E e A respectivamente, vem comigo :D

+ ∑ M E = 0 :     - 42 A + 37,5   x   8 + 23,5   x   32 - 9,5   x   32 = 0 A = 32,2857   k i p s ↑ A + ∑ M A = 0 :     - 42 E + 4,5   x   8 + 18,5   x   32 - 32,5   x   32 = 0 E = 39,7143   k i p s   ↑

Então temos:

A para B: 32,2857   k i p s

B para C: 32,2857 - 8 = 24,2857   k i p s

C para D: 24,2857 - 32 = - 7,7143   k i p s

D para E: - 7,7143 - 32 = - 39,7143   k i p s

Então podemos esboçar o esforço cortante vejam :D

Passo 3

Agora temos que calcular a área das seções :D

Áreas:

A para B: 4   x   32,2857 = 145,286   k i p . f t

B para C: 14   x   24,2857 = 340   k i p . f t

C para D: 14   x   - 7,7143 = - 108   k i p . f t

D para E: 9,5   x   - 39,7143 = - 377,286   k i p . f t

Passo 4

Agora precisamos determinar os e depois temos que desenhar o diagrama dos momentos calculados, partiu!!!

M A = 0 M B = 0 + 145,286 = 145,286   k i p . f t M C = 145,286 + 340 = 485,29   k i p . f t M D = 485,29 - 108 = 377,29   k i p . f t M E = 377,28 - 377,286 = 0

Máximo M = 485,29 k i p . f t = 5,2834   x   10 3 k i p . i n         σ a l l = 22 k s i

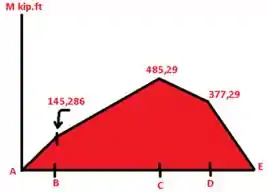
Passo 5

Agora podemos determinar determine a largura mínima b do flange que poderá ser usada.

S m i n = M σ a l l = 5,2834   x   10 3 22 = 264,70   i n 3 I = 1 12   x   3 4   x   19 3 + 2 1 2   x   b   x   1 3 + b   x   1   x   10 2 = 428,69 + 200,17 b C = 9,5 + 1 = 10,5   i n S m i n = 1 c = 40,828 + 19,063 b = 264,70

E b:

b = 11,74   i n

Resposta

b = 11,74   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que P = 12k N , trace os diagramas de força cortante e momento fletor para a viga A B e determine a tensão normal máxima provocada pelo momento fletor.
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados na figura, e determine a tensão normal máxima gerada pelo momento fletor.
Sabendo que P = Q = 480N , determine (a) a distância para a qual o valor absoluto do momento de flexão na viga é o menor possível, (b) a correspondente tensão normal máxima em razão da flexão. (veja a
Determine (a) a distância para a qual o valor absoluto do momento de flexão na viga é o menor possível, (b) a correspondente tensão normal máxima em razão da flexão. (veja a sugestão do problema 5.27)
Uma barra de seção transversal circular cheia, com diâmetro d e feita de aço, está vinculada, conforme mostra a figura. Sabendo que para o aço ρ = 7697 k g m 3 , determine o menor diâmetro d que pode