Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 161

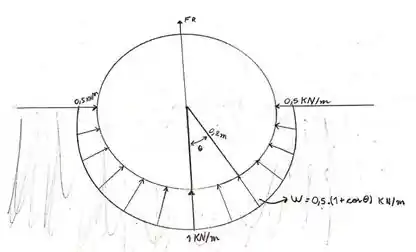
Se a distribuição da reação do solo sobre o tubo por metro de comprimento pode ser aproximada como mostrado, determine a intensidade da força resultante devido a esse carregamento.

Passo 1

No primeiro momento você pode até se sentir perdido, mas vamos por partes, a gente pode dividir o problema nas forças verticais e horizontais:

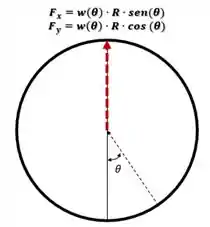
Então, as integrais do problema são:

F x = ∫ - π 2 π 2 0,5 1 + c o s θ × 0,8 × s e n θ   d θ

F y = ∫ - π 2 π 2 0,5 1 + c o s θ × 0,8 × c o s θ   d θ

Repare que os limites de integração são - π / 2 até π / 2 , considerando o semi-círculo do problema com relação ao ângulo θ sendo medido como foi dado no desenho da questão e no esquema acima.

Passo 2

Bora integrar esses caras aí... antes, vou só dar uma ajeitada nas integrais para ficar mais fácil:

F x = ∫ - π 2 π 2 0,4 1 + c o s θ × s e n θ   d θ = ∫ - π 2 π 2 0,4 s e n θ d θ + ∫ - π 2 π 2 0,4 c o s θ s e n θ d θ

F y = ∫ - π 2 π 2 0,4 1 + c o s θ c o s θ   d θ = ∫ - π 2 π 2 0,4 c o s θ   d θ + ∫ - π 2 π 2 0,4 cos 2 ⁡ θ d θ

Agora sim, vamos resolver cada termo dessas integrais!

Passo 3

A nossa F x é dada por:

F x = ∫ - π 2 π 2 0,4 s e n θ d θ + ∫ - π 2 π 2 0,4 c o s θ s e n θ d θ

Calculando a primeira integral...

∫ - π 2 π 2 0,4 s e n θ d θ = - 0,4 c o s θ | π / 2 - π / 2

= - 0,4 cos ⁡ π 2 - cos ⁡ - π 2 = - 0,4 0 - 0 = 0

Show de bolê, agora a segunda integral:

∫ - π 2 π 2 0,4 c o s θ s e n θ d θ

Aqui vamos precisar usar alguma identidade trigonométrica... olhando numa tabela com algumas (aqui no responde aí, na parte de cálculo tem essa tabela pra você olhar ;) ) encontrei uma relação aqui:

s e n 2 θ = 2 s e n θ cos ⁡ θ

Logo...

s e n θ cos ⁡ θ = s e n 2 θ 2

Substituindo:

∫ - π 2 π 2 0,4 c o s θ s e n θ d θ = 0,4 2 ∫ - π 2 π 2 s e n 2 θ d θ

Aplicando uma substituição simples:

u = 2 θ

d u = 2 d θ ∴ d θ = d u 2

0,4 2 ∫ - π 2 π 2 s e n 2 θ d θ = 0,4 4 ∫ s e n u d u

= - 0,1 × cos ⁡ u

= - 0,1 c o s ⁡ ( 2 θ ) π / 2 - π / 2

= - 0,1 cos ⁡ π - cos ⁡ - π

= - 0,1 - 1 - - 1 = - 0,1 0 = 0

Assim a gente conclui que:

F x = ∫ - π 2 π 2 0,4 s e n θ d θ + ∫ - π 2 π 2 0,4 c o s θ s e n θ d θ = 0 + 0 = 0

Passo 4

Então nossa resultante em F x deu zero, mas e a nossa F y , vamos calculá-la.

F y = ∫ - π 2 π 2 0,4 c o s θ   d θ + ∫ - π 2 π 2 0,4 cos 2 ⁡ θ d θ

Começando pela primeira integral de F y que é...

∫ - π 2 π 2 0,4 cos ⁡ θ d θ = 0,4 s e n θ π / 2 - π / 2

= 0,4 s e n π 2 - s e n - π 2

= 0,4 1 - - 1

= 0,4 2 = 0,8

Agora para fechar, o nosso segundo termo de F y

∫ - π 2 π 2 0,4 cos 2 ⁡ θ d θ

Novamente, vamos precisar de alguma identidade trigonométrica, a que vamos usar aqui é:

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

Substituindo:

∫ - π 2 π 2 0,4 cos 2 ⁡ θ d θ = 0,4 2 ∫ - π 2 π 2 1 + cos ⁡ 2 θ d θ

= 0,2 ∫ - π 2 π 2 d θ + ∫ - π 2 π 2 cos ⁡ 2 θ d θ

Beleza, aqui temos agora duas integrais para resolver... a primeira que é mais rápida vai ficar:

∫ - π 2 π 2 d θ = θ π 2 - π 2

= π 2 - - π 2 = π

E a segunda vamos ter:

∫ - π 2 π 2 cos ⁡ 2 θ d θ

Aplicando uma substituição simples:

u = 2 θ

d u = 2 d θ ∴ d θ = d u 2

∫ - π 2 π 2 cos ⁡ 2 θ d θ = 1 2 ∫ cos ⁡ u d u

= 1 2 s e n u d u = 1 2 s e n ( 2 θ ) π / 2 - π / 2

= 1 2 s e n π - s e n - π

= 1 2 0 - 0 = 0

Agora, retornando para o que tínhamos:

∫ - π 2 π 2 0,4 cos 2 ⁡ θ d θ = 0,2 ∫ - π 2 π 2 d θ + ∫ - π 2 π 2 cos ⁡ 2 θ d θ = 0,2 π + 0 = 0,2 π

E esse valor vamos retornar para encontrar o valor da F y

F y = ∫ - π 2 π 2 0,4 c o s θ   d θ + ∫ - π 2 π 2 0,4 cos 2 ⁡ θ d θ

F y = 0,8 + 0,2 π = 1,428 k N

Resposta

F x = 0

F y = 1,428 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em que ângulo θ uma força de 800N deve ser aplicada para que a resultante R das duas forças tenha um módulo de 2000N ? Para esta condição, determine o ângulo β entre R e a vertical.
Os cabos de sustentação A B e A C estão presos no topo da torre de transmissão. A força trativa no cabo A C vale 8k N . Determine a força trativa T necessária no cabo A B , tal que o efeito resultante
No projeto de um robô para colocar, sem folga, a pequena parte cilíndrica em um furo circular, o braço do robô deve exercer uma força P de 90N na peça, paralelamente ao eixo do furo, como mostrado. De
Em que ângulo θ deve ser aplicada uma força de 400N , para que a resultante R das duas forças tenha um módulo de 1000N ? Para essa condição, qual será o ângulo β entre R e a horizontal?
O cabo A B evita que a barra O A gire no sentido horário em torno do pivô O . Se a força trativa no cabo vale 750N , determine os componentes n e t desta força, atuando no ponto A da barra.