Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 78
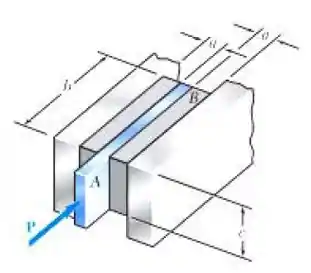
Dois blocos de borracha com um módulo de elasticidade transversal são colados a dois suportes rígidos e a uma placa . Sabendo que , determine a maior força admissível e a menor espessura admissível dos blocos para que a tensão de cisalhamento na borracha não exceda 1,5 MPa e o deslocamento da placa seja no mínimo .
Passo 1
E ai gurizada tudo belezinha??? O enunciado pede que primeiramente a gente determine a maior força admissível e o deslocamento da placa, para facilitar os cálculos e a gente visualizar melhor vamos desenhar um diagrama de corpo livre deste elemento :D
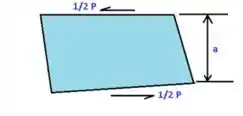
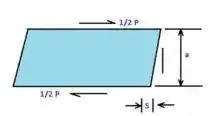
Sabendo que a Tensão de cisalhamento é dada por:
Isolando P temos:
Passo 2
Então para se obter a menor dimensão basta isolarmos “a” da equação de Tensão de cisalhamento abaixo:
Resposta
Exercícios de Livros Relacionados
A haste é feita de alumínio 2014 -T 6 . Se for submetida à carga de tração de 700N e tiver diâmetro de 20mm , determine a deformação por cisalhamento máxima absoluta na haste em um ponto sobre sua sup
Determine o módulo de compressibilidade para borracha dura se E b = 5GPa e ν b = 0,43 .
As tensões principais no plano e as deformações associadas em um plano em um ponto são σ 1 = 250MPa , σ 2 = 112MPa , ϵ 1 = 1,02 ( 10 - 3 ) , ϵ 2 = 0,180 ( 10 - 3 ) . Determine o módulo de elasticidade
O vaso de pressão esférico tem diâmetro de 2 m e espessura de 10 mm. Um extensômetro com 20 mm de comprimento é ligado ao vaso e constata-se um aumento no comprimento de 0,012 mm quando o vaso é press
A seção retangular da viga retangular é submetida a um momento M. Determine uma expressão para um aumento no comprimento das retas AB e CD. O material tem módulo de elasticidade E e coeficiente de Poi