Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 12

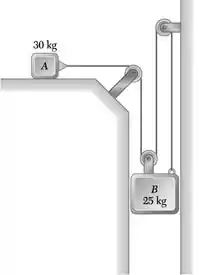
Os dois blocos mostrados na figura estão originalmente em repouso. Desprezando as massas das roldanas e o efeito do atrito nessas roldanas e considerando que os coeficientes de atrito entre ambos o bloco A e a superfície horizontal são μ s = 0,25 e μ k = 0,20, determine (a) a aceleração de cada bloco e (b) a tração no cabo

Passo 1

Do diagrama

x A + 3 y B = constante

Então

v A + 3 v B = 0

a A + 3 a B = 0

a A = - 3 a B

Passo 2

Primeiro determine se os blocos se moverão com aA = aB = 0. Temos

A:

+ ↓ Σ F y = 0 :           W B - 3 T = 0           ou           T = 1 3 m B g

B:

← + Σ F x = 0 :           F A - T = 0

Então

F A = 1 3 × 25   kg × 9.81   m/ s 2 = 81.75   N

+ ↓ Σ F y = 0 :           W A - N A = 0             ou             N A = m A g

Passo 3

Além disso

F A max = μ s A N A = μ s A m A g = 0.25 × 30   kg × 9.81   m/ s 2

= 73.575   N

FA > (FA)max que implica que os blocos se moverão.

Passo 4

  1. A:

    2. + ↓ Σ F y = 0 :             W A - N A = 0             ou             N A = m A g

    Deslizante:

    F A = μ k A N A = 0.20   m A g

    ← + Σ F x = m A a A :             F A - T = m A a A

    Usando a Eq. (1)

    T = 0.20   m A g + 3 m A A B

    B:

    + ↓ Σ F y = m B a B :             W B - 3 T = m B a B

    ou

    m B g - 3 0.20   m A g + 3 m A a B = m B a B

    ou

    a B = g 1 - 0.6 m A m B 1 + 9 30   kg 25   kg

    = 0.23278   m/ s 2

    Passo 5

  2. Nós temos

T = 30   k g 0.20 × 9.81 + 3 × 0.23278   m/ s 2

Resposta

a )   a A = 0.698   m/ s 2 →

a A = 0.233   m/ s 2 ↓

b )   T = 79.8   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A aceleração devida à gravidade na Lua é de 1,62 m/s2. Determine (a) o peso em newtons, (b) a massa em quilograma na Lua de uma barra de ouro, cuja massa foi oficialmente definida como 2 kg.
Sabendo que o sistema mostrado começa do repouso, encontre a velocidade em t = 1,2 s de (a) colar A, (b) colar B. Despreze as massas das polias e o efeito do atrito.
Uma balança de mola A e uma balança de alavanca B com braços de alavanca iguais estão presas ao teto de um elevador e pacotes idênticos estão sendo segurados por elas, tal como mostra a figura. Sabend
O valor da aceleração da gravidade g em qualquer latitude ϕ pode ser dado pela fórmula g = 9,7087 1 + 0,0053sen 2 ϕ m/ s 2 onde o efeito da rotação da Terra e também o fato de que a Terra não ser esfé
Para transportar uma série de feixes de telhas A para um telhado, um empreiteiro usa um elevador motorizado que consiste em uma plataforma horizontal BC que se desloca em trilhos presos às laterais de