Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 89
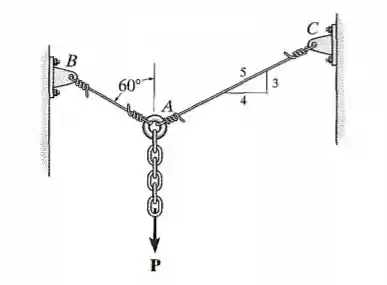
Os dois cabos de aço e são usados para suportar a carga. Se ambos tiverem uma tensão de tração admissível , e se o cabo tiver diâmetro de e o cabo tiver diâmetro de , determine a maior força P que pode ser aplicada à corrente antes que um dos cabos falhe.
Passo 1
Oláaaa, querido! Cê tá bem?
Então, o problema nos fornece o valor da tensão normal admissível de cada cabo e pede o valor máximo de antes que um dos cabos falhe. Quem falha primeiro é o cabo mais fraco né?
Então máximo vai acontecer quando o cabo mais fraco estiver suportando a sua força normal máxima. Aí para descobrir quem é o cabo mais fraco a gente precisa descobrir a força máxima de cada cabo primeiro.
Temos essa expressão para a tensão admissível :
Podemos achar a força máxima que um cabo resiste através dela, isolando :
Então para achar a força que cada cabo aguenta, vamos usar essa expressão. Bora!
Passo 2
Para o cabo ela fica
Como ele tem seção circular, a área é dada por:
Vamos ter:
E para o cabo vamos ter algo parecido:
Percebe que a menor força é do cabo . Então ele é o mais fraco. E é quando quem temos o nosso máximo. Vamos descobrir esse !
Passo 3
Para achar vamos usar a segunda lei de Newton no nó A. Então vamos fazer aquele diagrama de corpo livre esperto:
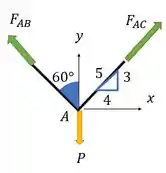
A equação para o eixo fica:
Aí lembra que queremos o valor de para
Passo 4
Agora a equação para o eixo :
Substituindo os valores das forças: