Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 10

Faça um gráfico da intensidade da tensão de cisalhamento distribuída na seção transversal da escora se ela for submetida a uma força de cisalhamento V = 15 k N .

Passo 1

Dados da questão: V = 15   k N

A questão pede: O gráfico de cisalhamento.

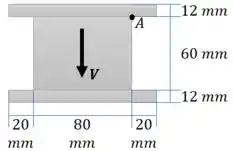
Para calcular a tensão de cisalhamento usaremos a Equação 7.3, e pra aplicar essa equação vamos precisar calcular o Momento de Inércia ( I ) e o Momento Estático ( Q ) . Não será preciso calcular o centroide, pois como a figura é perfeitamente simétrica o centroide fica no centro.

Por definição, a tensão de cisalhamento parte do zero e cresce ao longo da seção de maneira parabólica e crescente até o centroide, e depois decrescesse até zero novamente.

Mas observe que a nossa seção possui uma mudança brusca de espessura. O resultado disso é que na região da mudança de espessura, iremos calcular a seção duas vezes, considerando cada uma das espessuras. O resultado final será um gráfico semelhante a imagem abaixo:

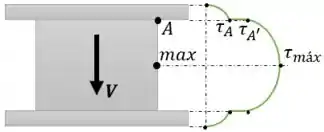
O nosso objetivo será calcular essas três tensões em destaque!

Passo 2

Vamos começar calculando o Momento de Inércia!

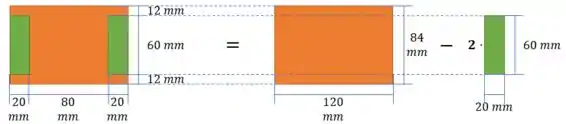
Observe a figura abaixo. Podemos facilmente calcular o momento de inércia da figura, subtraindo o momento de inércia da figura laranja pelas duas figuras verdes.

I = I l a r a n j a - 2 ⋅ I v e r d e

I = 120 ⋅ 84 3 12 - 2 ⋅ 20 ⋅ 60 3 12

I = 5207040   m m 4

Passo 3

Agora vamos calcular os Momentos Estáticos nos pontos de interesse.

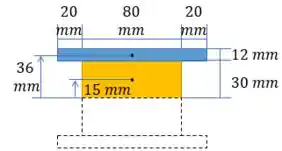
O primeiro ponto de interesse é o ponto A. O momento estático é representado pela área em azul abaixo:

Q A = A a z u l ⋅ y a z u l

Q A = 12 ⋅ 120 ⋅ 36

Q A = 51840   m m 3

Momento estático máximo:

Q m á x = Q a z u l + Q a m a r e l a

Q m á x = A a z u l ⋅ y a z u l + A a m a r e l o ⋅ y a m a r e l o

Q m á x = 12 ⋅ 120 ⋅ 36 + 30 ⋅ 80 ⋅ 15

Q m á x = 87840   m m 3

Passo 4

Agora basta aplicar a Equação 7.3 nos pontos de interesse

PONTO A :

τ A = V Q A I t A

τ A = 15 ⋅ 10 3 N ⋅ 51840   m m 3 5207040   m m 4 ⋅ 120 m m

τ A = 1,24   M P a

PONTO A ’ :

τ A ' = V Q A I t A '

τ A ' = 15 ⋅ 10 3 N ⋅ 51840   m m 3 5207040   m m 4 ⋅ 8 0 m m

τ A ' = 1,87   M P a

PONTO MÁXIMO:

τ m á x = V Q m á x I ⋅ t m á x

τ m á x = 15 ⋅ 10 3 N ⋅ 87840   m m 3 5207040   m m 4 ⋅ 80 m m

τ m á x = 3,16   M P a

Passo 5

Agora só aplicar os valores no nosso gráfico:

Resposta

τ A = 1,24   M P a

τ A ' = 1,87   M P a

τ m á x = 3,16   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Uma viga extrudada tem seção transversal como mostrado e uma espessura de parede constante e igual a 3 m m . Para uma força cortante vertical de 10 k N , determinar:A tensão de cisalhamento no ponto A
Uma viga extrudada tem seção transversal como mostrado e uma espessura de parede constante e igual a 3 m m . Para uma força cortante vertical de 10 k N , determinar:A máxima tensão de cisalhamento na
Uma viga com a seção transversal mostrada é submetida a uma força cortante vertical V . Determine (a) a linha horizontal ao longo da qual a tensão de cisalhamento máxima. (b) a constante k na expressã
A viga fabricada mostrada é feita colando duas tiras de madeira compensada de 20 x 250 mm e duas pranchas de 50 x 100 mm. Sabendo que a tensão de cisalhamento média nas juntas coladas é de 350 kPa, de