Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 7
Os dois cabos estão interligados em A. Se a força P provocar um deslocamento horizontal de 2 mm no ponto em A, calcule a deformação em cada cabo.
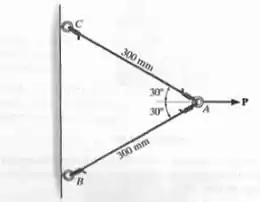
A, determine a deformação normal desenvolvida em cada cabo.
Passo 1
Primeiramente, vamos vizualizar a situação. Devido à simetria, o que a contece em AB, também acontece em AC, logo:
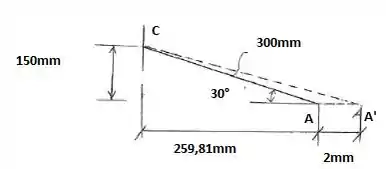
O 259,81 foi obtido fazendo-se
Podemos calcular o tamanho do lado tracejado (comprimento final) por Pitágoras. Logo:
=
Passo 2
Com o comprimento final e inicial calculados, teremos a deformação utilizando a relação:
Resposta
Exercícios de Livros Relacionados
O raio original do tubo curvado é 0,6 m . Se ele sofrer aquecimento não uniforme que provoque uma deformação normal ao longo de seu comprimento ∈ = 0,08 sen θ , determine o aumento no comprimento do
O raio original do tubo curvado é 0,6 m . Se ele sofrer aquecimento não uniforme que provoque uma deformação normal ao longo de seu comprimento ∈ = 0,05 cos θ , determine o aumento no comprimento do
Um cabo fino é enrolado ao longo da superfície cuja forma é y =0,02x², onde x e y são dados em mm. A posição original da extremidade B é x = 250 mm. Se o cabo sofrer uma deformação normal∈ = 0,0002x a
A fibra A B tem comprimento L e orientação θ . Se suas extremidades A e B sofrerem deslocamentos muito pequenos u A e v B , respectivamente, determine a deformação normal na fibra quando ela estiver n
Um corpo de prova com comprimento original de 300m m tem diâmetro original de 12m m e é submetido a uma força de 2,5k N . Quando a força é aumentada para 9k N , o corpo de prova sofre um alongamento d