Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 130
Dois cabos estão ligados juntos a C e carregados como mostra a figura. Determine a tensão no cabo AC, no cabo BC.
Passo 1
Vamos começar o exercício desenhando o diagrama de corpo livre para o ponto C:
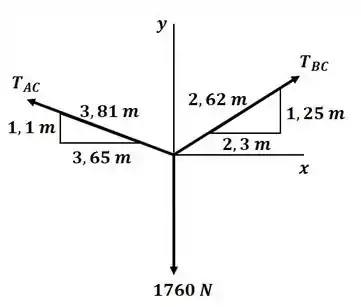
Passo 2
Agora vamos aplicar o somatório de forças na direção para o DCL do passo 1:
Agora vamos aplicar o somatório de forças na direção :
Passo 3
Substituindo a expressão encontrada para nessa última equação, temos:
Agora, substituindo o valor de na expressão encontrada para :
Resposta
Exercícios de Livros Relacionados
Determine o comprimento necessário L da corrente entre A e B, e a força trativa correspondente em A, se a inclinação da corrente for horizontal quando ela entra na guia em A. O peso da corrente vale 1
Diversas bóias esféricas estão igualmente espaçadas e rigidamente presas a um cabo flexível de 20m de comprimento. As extremidades A e B estão ancoradas a 16m de distância no fundo de um lago de água
Muitos pequenos dispositivos de flutuação estão presos a um cabo e a diferença entre a flutuação e o peso resulta em uma força direcionada para cima de 30N por metro do comprimento do cabo. Determine
Uma corda de 40m de comprimento está suspensa entre dois pontos que estão separados por uma distância horizontal de 10 m. Calcule a distância h até o ponto mais baixo da corda.
Sob vento fraco, o dirigível está amarrado ao guincho no solo por 100 m de um cabo de 12 m m que tem uma massa de 0,51 k g / m . Um torque de 400N no tambor é necessário para iniciar o enrolamento do