Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 177
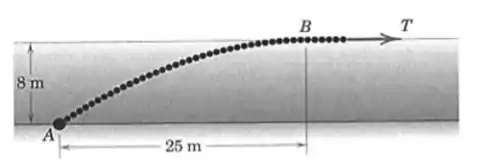
Muitos pequenos dispositivos de flutuação estão presos a um cabo e a diferença entre a flutuação e o peso resulta em uma força direcionada para cima de por metro do comprimento do cabo. Determine a força que deve ser aplicada para impor ao cabo a configuração mostrada.
Passo 1
Primeiro vamos anotar as informações que a questão anterior e a imagem nos oferecem, para facilitar a visualização:
= 0m
8m
Passo 2
Temos que pela figura, o nosso em B vale . Logo, podemos jogar na equação da posição!
A única solução numérica para isso é que
Passo 3
Sabemos então que:
Resposta
Exercícios de Livros Relacionados
Se α = 120 ° ,β90 ° ,γ = 60° e F = 400N , determine a intensidade e os ângulos de direção coordenados da força resultante que atua sobre o gancho.
Determine a intensidade e os ângulos de direção coordenados de F 2 , de modo que a resultante das duas forças seja zero.
O poste está submetido à força F , que tem componentes atuando ao longo dos eixo x , y , z , como mostra a figura. Se a intensidade de F é 3 kN, β = 30 ° e γ = 75 ° , determine as intensidades de suas
O poste está submetido à força F , que tem componentes F x = 1,5 kN e F z = 1,25 kN. Se β = 75 ° , determine as intensidades de F e F y .
Se a força resultante que atua sobre o suporte é direcionada ao longo do eixo y positivo, determine a intensidade da força resultante e os ângulos de direção coordenados de F , de modo que β90 ° .