Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 158

Diversas bóias esféricas estão igualmente espaçadas e rigidamente presas a um cabo flexível de 20   m de comprimento. As extremidades A e B estão ancoradas a 16   m   de distância no fundo de um lago de água doce, a profundidade de 8   m . As bóias e o cabo têm um peso combinado de 100   N por metro de comprimento do cabo e a flutuação delas na água produz uma força direcionada para cima de 560   N por metro de comprimento do cabo. Calcule a profundidade h abaixo da superfície, do topo da linha de bóias. Ache, também, o ângulo θ feito pela linhas de bóias com a horizontal em A.

Passo 1

Primeiro vamos anotar as informações que a questão anterior e a imagem nos oferecem, para facilitar a visualização:

y A - y b = 1 6   m

μ = 560 - 100 = 460   N / m

s = 20   m

O esquemático da questão segue abaixo:

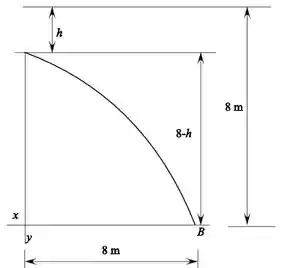
Como vemos pelo esquemático, vamos tratar de começo somente de uma metade nossa figura.

Passo 2

Temos que o comprimento da nossa corda é de 20   m , mas se pegarmos somente metade da corda temos que ela é 10   m . Daí aplicamos na fórmula para acharmos o T 0 .

s = T 0 μ sinh ⁡ μ x T o

10 = T 0 460 sinh ⁡ 460   ( 8 ) T o

Para isso, temos:

T 0 = 3110   N

Passo 3

Então essa é a força trativa mínima!! Agora vamos achar a força trativa em A.

T = T 0 cosh ⁡ μ x T 0 = 3310   cosh ⁡ 460 ( 8 ) 3110

T a = 5550   N

Agora aplicamos na equação abaixo para acharmos a posição y aplicado para T A .

T = T 0 + μ y

5550 = 3110 + 460 y

y = 5.31

Logo:

h = 8 - 5.31 = 2.69   m

Passo 4

Para acharmos o ângulo, temos que:

d y d x = tan ⁡ θ = sinh ⁡ μ x T 0

tan ⁡ θ = sinh ⁡ 460 ( 8 ) 3110 = 55.9 °

Resposta

h = 2.69   m

θ = 55.9 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A engrenagem está submetida às duas forças caudadas pelo contato com outras engrenagens. Determine a resultante das duas forças e expresse o resultado como um vetor cartesiano.
Se a força resultante que atua sobre o gancho é F R = 200 i + 800 j + 150 k N, determine a intensidade e os ângulos de direção coordenados de F .
Se a força resultante que atua sobre o suporte precisa ser F R = 800 jN , determine a intensidade e os ângulos de direção coordenados de F .
Determine a intensidade e os ângulos de direção coordenados de F 2 , de modo que a resultante das duas forças atue ao longo do eixo x positivo e tenha uma intensidade de 500 N.
O eixo S exerce três componentes de força sobre a ferramenta D . Encontre a intensidade e os ângulos de direção coordenados da força resultante. A força F 2 atua dentro do octante mostrado.