Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 159
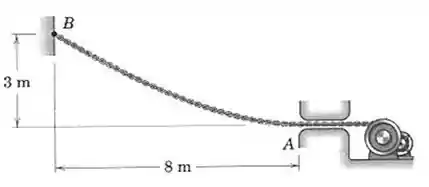
Determine o comprimento necessário da corrente entre A e B, e a força trativa correspondente em A, se a inclinação da corrente for horizontal quando ela entra na guia em A. O peso da corrente vale por metro de seu comprimento.
Passo 1
Primeiro vamos anotar as informações que a questão anterior e a imagem nos oferecem, para facilitar a visualização:
= 3m
Passo 2
Temos que pela figura, o nosso em B vale . Logo, podemos jogar na equação da posição!
Passo 3
Daqui basta pegarmos essa força trativa e jogar na fórmula do comprimento do cabo!
Resposta
Exercícios de Livros Relacionados
A força F atua sobre o suporte dentro do octante mostrado. Se as intensidades das componentes x e z de F são F x = 300N e F z = 600 N , respectivamente, e β = 60 ° , determine a intensidade de F e de
Determine os ângulos de direção coordenados da força F 1 e os indique na figura.
O mastro está submetido às três forças mostradas. Determine os ângulos de direção coordenados α 1 , β 1 , γ 1 de F 1 , de modo que a força resultante que atua no mastro seja zero.
Se a força resultante que atua sobre o suporte é F R = - 300 i + 650 j + 250 kN , determine a intensidade e os ângulos de direção coordenados de F .
O mastro está submetido às três forças mostradas. Determine os ângulos de direção coordenados α 1 , β 1 , γ 1 de F 1 , de modo que a força resultante que atua no mastro seja F R = 350 iN .