Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 46
Dois cabos estão ligados em C e são carregados como mostra a figura. Determine a tração no cabo AC e no cabo BC.
Passo 1
Tá legal, vamos lá! Antes de começar o exercício, é sempre bom ter em mente as dicas que o próprio livro nos dá antes de cada seção de exercícios, na parte de “metodologia para resolução de problemas”. Então beleza, seguindo aquelas dicas, vamos começar fazendo o diagrama de corpo livre no ponto C:
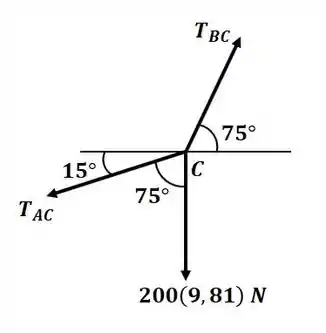
Passo 2
Agora que temos o DCL do problema, e temos somente três forças, vamos desenhar o triângulo de forças do sistema para descobrir os valores das tensões:
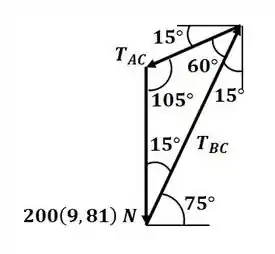
Agora ficou fácil, só precisamos aplicar a lei dos senos para esse triângulo, que será:
Passo 3
Para resolver a letra , vamos pegar a seguinte parcela da equação acima:
Resolvendo a equação:
E, para a letra , a mesma coisa, só que pegando a outra parcela da equação:
Resolvendo a equação: