Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 143

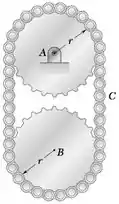
Dois discos, cada um de massa m e raio r estão ligados como mostra a figura por uma corrente contínua de massa desprezível. Se um pino no ponto C da corrente é repentinamente removido, determine (a) a aceleração angular de cada disco, (b) a tração na porção esquerda da corrente, (c) a aceleração do centro do disco B.

Passo 1

Cinemática:

Assuma   α A                 e               α B  

ω A = ω B = 0

a D = r α A ↓

a E = a D = r α A ↓

a - B = a E + a B / E = r α A + r α B

a - B = r α A + α B ↓

Passo 2

Cinética:

Disco A:

+ Σ M A = Σ M A eff:           T r = I - α A

T r = 1 2 m r 2 α A

α A = 2 T m r

Passo 3

Disco B:

+ Σ M B = Σ M B eff:           T r = I - α B

T r = 1 2 m r 2 α B

α B = 2 T m r

De (1) e (2), notamos que α A = α B

+ Σ M E = Σ M E eff:           W r = I - α B + m a - B r

W r = 1 2 m r 2 α B + m r α A + α B r

α A = α B :               W r = 5 2 m r 2 α A

Substitua por α A em (1):

2 5 g r = 2 T m r

a B = r α A + α B = r 2 α A = 2 r 2 5 g r

Resposta

α A = 2 5 g r

α B = 2 5 g r

T = 1 5 m g

a B = 4 5 g ↓

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma haste uniforme de comprimento L e massa m é apoiada como mostra a figura. Se o cabo ligado a B repentinamente se parte, determine: (a) a aceleração da extremidade B, (b) a reação no suporte do pin
Uma haste fina e uniforme de comprimento L = 36 pol. e peso W = 4 lb pende livremente de uma dobradiça em A. Se uma força P de magnitude 1,5 lb for aplicada em B horizontalmente à esquerda (h = L), de
Duas barras uniformes, ABC de massa 3 kg e DCE de massa 4 kg são ligadas por um pino C e por duas cordas BD e BE. O conjunto em forma de T gira em um plano vertical sob o efeito combinado da gravidade
Uma haste delgada de 1,5 kg é soldada a um disco uniforme de 5 kgcomo mostra a figura. O conjunto oscila livremente em torno de Cem um plano vertical. Sabendo que na posição mostrada na figura oconjun
Uma haste uniforme de comprimento L e massa m é apoiada como mostra a figura. Se o cabo ligado a B repentinamente se parte, determine: (a) a aceleração da extremidade B, (b) a reação no suporte do pin