Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 120

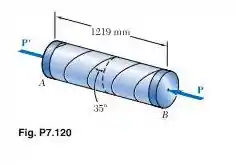
Um vaso de pressão com diâmetro interno de 254   m m , espessura de 6,35 m m   e comprimento de 1219   m m   é soldado em espiral e possui duas tampas laterais rígidas. A pressão manométrica dentro do vaso é de 2069   k P a e são aplicadas forças axiais centradas P   e P '   de 44,5   k N   nas tampas laterais. Determine (a) a tensão normal perpendicular à solda e (b) a tensão de cisalhamento paralela à solda.

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora pra outra questão.

Primeiramente, sabemos que a tensão normal, para tubos de paredes finas sujeitos à pressão, é dada por:

σ 1 = p r t

σ 2 = p r 2 t

Onde p   é a pressão interna, r   é o raio interno e t   é a espessura da parede. Além disso, a primeira pressão é a pressão na direção radial e a segunda é a pressão na direção axial.

Logo, sabemos que:

r = 254 2 = 127 m m

t = 6,35   m m

Portanto:

σ 1 = 2,069 × 127 6,35 = 41,38   M P a

Como a tensão na direção axial é metade dessa, teremos:

σ 2 = 20,69   M P a

Passo 2

Agora, além da pressão, precisamos da tensão normal devido às forças P   e P ' .   Para isso, precisamos da área transversal, pois a tensão depende dela. Sabemos que o raio externo será:

r 0 = r + t = 127 + 6,35 = 133,35   m m

Portanto:

A = π r 0 2 - r 2 = π 133,35 2 - 127 2 = 5193,75   m m 2

A tensão normal devido às forças será:

σ = - P A

Substituindo:

σ = - 44,5 × 10 3 5193,75 = - 8,56   M P a

Esta tensão também atua axialmente.

Passo 3

Agora, vamos juntar os dados. Sabemos que a tensão axial será a soma das parcelas da pressão e das forças, a tensão radial será a encontrada no passo 1 e a tensão cisalhante será nula, pois não há cisalhamento. Portanto:

σ x = 20,69 - 8,56 = 12,13   M P a

σ y = 41,38   M P a

τ x y = 0

Agora, basta calcular os parâmetros do círculo de Mohr para determinarmos o que foi pedido.

Sabemos que a tensão média será:

σ m é d = 1 2 σ x + σ y = 53,51   M P a

Este será o centro do círculo. Já o raio, é dado por:

R = σ x - σ y 2 2 + τ x y

Substituindo:

R = 14,62   M P a

Passo 4

Com esses dados, basta usá-los para encontrar o que foi pedido. Sabemos que a tensão normal perpendicular a solda será:

σ x ' = σ m é d + R c o s 2 × 35 °

Não se esqueça de multiplicar o ângulo por 2, pois o círculo de Mohr sempre gira o dobro do ângulo de giro real. Logo:

σ x ' = 58,51   M P a

Passo 5

A letra b nos pede a tensão cisalhante. Ela será:

τ x y = R s e n 70 °

Logo:

τ x y = 13,73   M P a

Prontinho!

Resposta

  1. σ x ' = 58,51   M P a
  2. τ x y = 13,73   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tubo de aço inoxidável 304 tem espessura de 10m m . Se o torque aplicado for T = 50N ⋅ m , determine a tensão de cisalhamento média no tubo. Despreze as concentrações de tensão nos cantos. As dimens
O eixo quadrado é usado na extremidade de um cabo de acionamento para registrar a rotação do cabo em um medidor. Se tiver as dimensões mostradas na figura e for submetido a um torque de 8N ⋅ m , deter
O tubo é feito de plástico, tem 5m m de espessura, e as dimensões médias mostradas na figura. Determine a tensão de cisalhamento média nos pontos A e B se ele for submetido ao torque T=5N ⋅ m . Mostre
Um tubo com as dimensões mostradas na figura é submetido a um torque a T= 50N ⋅ m . Desprezando as concentrações de tensão em seus cantos, determine a tensão de cisalhamento média no tubo nos pontos A
Determine a espessura constante do tubo retangular se a tensão de cisalhamento média não pode ultrapassar 84M P a quando um torque T = 2,5k N ⋅ m for aplicado ao tubo. Despreze as concentrações de ten