Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 80

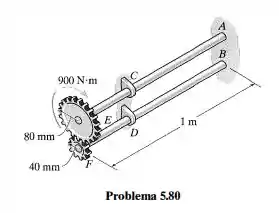
Os dois eixos de 1   m de comprimento são feitos de alumínio 2014 - T 6 . Cada eixo tem diâmetro de 30   m m e os dois estão acoplados pelas engrenagens presas a uma das extremidades de cada um deles. As outras extremidades de cada um dos eixos estão engastadas em apoios fixos em A e B . Além disso, os eixos estão apoiados em mancais em C e D , que permitem que eles girem livremente ao longo de suas linhas centrais. Se um torque de 900   N . m for aplicado à engrenagem que está mais acima, como mostra a figura, determine a tensão de cisalhamento máxima em cada eixo.

Passo 1

Olá pessoal. Vamos resolver essa questão?

Essa questão quer saber a tensão de cisalhamento máxima em cada eixo, e como já sabemos, num tubo com secção transversal e material homogêneos em toda sua extensão, a tensão de cisalhamento máxima ocorrerá no ponto que o torque é máximo.

τ m á x = T m á x ⋅ c J  

Ou seja, em cada eixo, a tensão de cisalhamento máxima ocorrerá onde o torque for máximo. Agora nos resta determinas quais torques são esses.

Os dados que a questão nos forneceu foram os seguintes:

T E = 900   N ⋅ m

L E A = 1   m

R E = 80   m m = 0,08   m

R F = 40   m m = 0,040   m

L F B = 1   m

D = 30   m m = 0,030   m

Cálculo do Momento polar de inércia:

J = π 2 ⋅ c 4

J = π 2 ⋅ 0,030 2 4

J = 7,952 ⋅ 10 - 8   m 4

Passo 2

Devemos realizar o somatório dos momentos em ambos os eixos. Os dois eixos sofrem um momento gerado por uma força F que é resultante da ação do torque de 900   N ⋅ m no contato das engrenagens. Observando a imagem a seguir podemos ter uma ideia melhor de como fica o somatório.

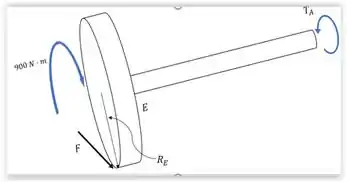
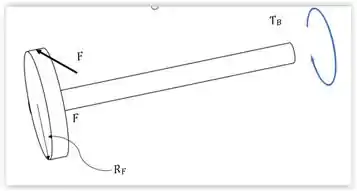
Realizando o somatório de torques primeiramente na sessão A E :

⟲ +     ∑ T = 0

T A - 900 + F ⋅ 0,08 = 0

Agora realizando o mesmo procedimento para sessão F B :

⟳ +     ∑ T = 0

T B - F ⋅ 0,04   = 0

T B = F ⋅ 0,04  

2 ⋅ T B = F ⋅ 0,08  

Utilizando essa relação entre T B e F no somatório de momento da primeira sessão temos:

T A - 900 + 2 ⋅ T B = 0

T A + 2 ⋅ T B = 900

Agora é necessária outra relação entre T A e T B para obter seus respectivos valores. E essa relação obteremos com o ângulo de torção em cada engrenagem. A ângulo de torção de uma engrenagem multiplicada pelo seu raio é o mesmo que o ângulo de torção da engrenagem que está acoplada multiplicada pelo raio desta:

ϕ F ⋅ R F = ϕ E ⋅ R E

ϕ F ⋅ 40 = ϕ E ⋅ 80

Como a deformação ϕ é dada por:

ϕ = T L J G

Temos a seguinte relação:

T B L B J G ⋅ 40 = T A L A J G ⋅ 80

T B ⋅ 40 = T A ⋅ 80

T B = T A ⋅ 2

Com essa relação se torna possível resolver a primeira relação:

T A + 2 ⋅ T A ⋅ 2 = 900

5 ⋅ T A = 900

T A = 180   N ⋅ m

T B = 180 ⋅ 2

T B = 360   N ⋅ m

Passo 3

A tensão de cisalhamento máxima no eixo F B :

τ m á x = T B ⋅ c J  

τ F B = 360   ⋅ 0,015 7,952 ⋅ 10 - 8  

τ F B =   67,91   M P a

A tensão de cisalhamento máxima no eixo A E :

τ m á x = T A ⋅ c J  

τ A E = 180   ⋅ 0,015 7,952 ⋅ 10 - 8  

τ A E =   33,95   M P a

Resposta

τ F B =   67,91   M P a

τ A E =   33,95   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As extremidades estriadas e engrenagens acopladas ao eixo de aço A-36 estão sujeitas aos torques mostrados. Determine o ângulo de torção da engrenagem C em relação à engrenagem D . O eixo tem diâmetro
A turbina desenvolve 150k W de potência, que é transmitida às engrenagens de tal modo que C e D recebem quantidades iguais. Se a rotação do eixo de aço A-36 de 100m m de diâmetro for ω=500r e v / m i
A turbina desenvolve 150k W de potência, que é transmitida às engrenagens de tal modo que C recebe 70% e D recebe 30%. Se a rotação do eixo de aço A-36 de 100m m de diâmetro for ω =800r e v / m i n u
O motor produz um torque T = 20N . m na engrenagem A . Se a engrenagem C travar repentinamente e parar de girar, mas B puder girar livremente, determine o ângulo de torção de F em relação a E e de F e
O motor transmite 33k W ao eixo de aço inoxidável 304 quando gira a 20H z . O eixo tem diâmetro de 37,5m m e está apoiado em mancais lisos em A e B , que permitem a livre rotação do eixo. As engrenage