Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 90
Resolva o Problema para a tensão de cisalhamento máxima no interior das regiões e e ângulo de torção da extremidade em relação à .
Passo 1
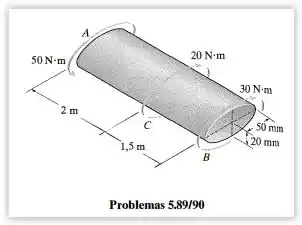
Nosso objetivo é determinar a tensão de cisalhamento máxima no interior das regiões e e o ângulo de torção da extremidade em relação à extremidade. Para isso teremos que determinar o torque em cada região. Até o passo é igual a questão passada, se você já respondeu, pule para o fim do passo 3.
Os dados que temos:
Para latão vermelho C83400, .
Passo 2
Primeiro vamos calcular os torques que atuam em cada região, para isso é dividiremos o tubo nessas regiões, resultando assim em:
Podemos observar que para o corpo de latão vermelho está em equilíbrio;
Já para a outra seção temos:
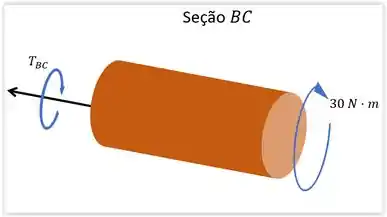
Sendo assim, para o corpo estar em equilíbrio:
Passo 3
Então agora só resta calcular as tensões de cisalhamento e o ângulo de torção.
A tensão de cisalhamento em uma elipse é dada por:
Logo para a seção ;
E para a seção ;
Ângulo de torção de uma elipse é dado por;
Ângulo de torção de ;