Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 11
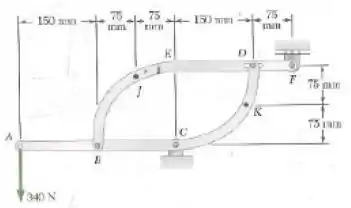
Dois elementos, cada qual consistindo em uma parte reta e um quarto de círculo, são unidos tal como mostra a figura e sustentam uma carga de em . Determine as forças internas ao ponto .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos calcular as reações em e em , com o equilíbrio do corpo inteiro:
Temos também que:
E:
Passo 2
Agora, vamos analisar as forças nas reações da barra :
E:
Passo 3
Podemos calcular as forças internas assumindo uma seção do ponto até . As forças internas sempre agem de forma normal e tangencial ao componente, seja uma barra ou, nesse caso, o arco semicircular. Então como o ponto é indicado em um ângulo, por geometria podemos concluir que esse ângulo é de :
Temos também que:
E:
Resposta
Exercícios de Livros Relacionados
5.47. O motor possui um peso de 4,25k N . Determine a força que cada corrente exerce sobre os ganchos em A, B e C. Despreze a dimensão dos ganchos e a espessura da viga.
5.42. Determine as reações de apoio do rolete A e o colar liso B na barra. O colar é fixo na barra AB, mas pode deslizar pela barra CD.
63.O carro sustenta o engradado uniforme com massa de 85k g . Determine as reações verticais sobre os roletes em A ,B e C . O rolete em B não é mostrado. Despreze massa do carro.
87. Uma mesa quadrada uniforme com peso W e lados a é sustentada por três pés verticais. Determine a menor força vertical P que pode ser aplicada em seu tampo que o fará tombar.
96. A prateleira simétrica está sujeita a uma carga uniforme de 4k P a . O apoio é fornecido por um parafuso (ou pino) localizado em cada extremidade A e A ' e por cantoneiras simétricas apoiadas cont