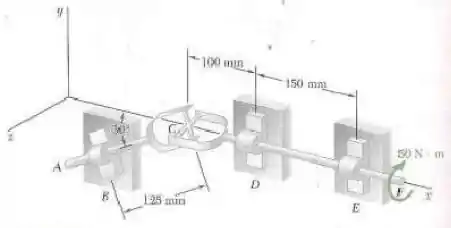
Dois eixos e , que estão no plano vertical , estão acoplados por uma junta universal em . Os mancais em e não exercem nenhuma força axial. Um binário de intensidade (no sentido horário quando visto a partir do eixo positivo) é aplicado ao eixo em . Em um dado instante, quando o braço da cruzeta preso ao eixo é horizontal, determine a intensidade do binário que deve ser aplicado ao eixo em para se manter equilíbrio, as reações em , e . (Dica: a soma dos binários exercidos sobre a cruzeta deve ser zero.)

Vamos analisar agora o eixo . Sabemos que em temos reações no eixo e no eixo . Considerando como a reação necessária em para manter o equilíbrio, temos que:

E:

Como as reações em são nulas, as reações em , também serão nulas.

Retornando ao eixo e calculando as reações, temos que:

Resolvendo e separando as componentes correspondentes, temos que:

:

:

Fazendo o somatório de forças, podemos encontrar as incógnitas que não foram encontradas:

Temos que:

E: