Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas Fundamentais - Ex. 5
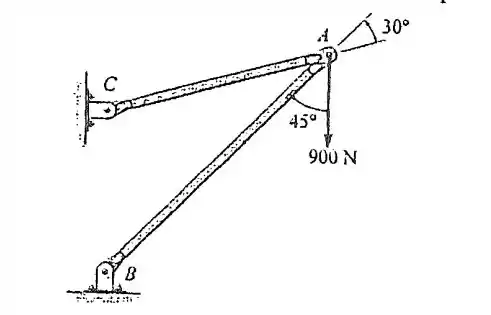
2.3. A força atua sobre a estrutura. Decomponha essa força nas componentes que atuam ao longo dos membros AB e AC, e determine a intensidade de cada componente.
Passo 1
Fala!
O que ele quer da gente é que achemos componentes da força de 900 N que passem pelas barras.
Com componentes, ele quer dizer que se somarmos vetorialmente essas duas forças, a resultante é 900 N. Então:
E repara que a força de está na direção do eixo vertical.
Para fazer um esquema dessa soma vetorial, a gente precisa pensar em como fazer vetores com a orientação de AB, AC e , formarem um triângulo. E respeitando também o sentido de .
A partir disso, nosso esquema fica assim:
Aí agora é descobrir esses F’s. Bora!
Passo 2
Vamos primeiro achar a componente da força em AB. Podemos usar lei dos senos:
Achando esses ângulos. Pela figura:
Logo:
Passo 3
Agora vamos achar a componente em AC. Pela lei dos senos: