Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 15
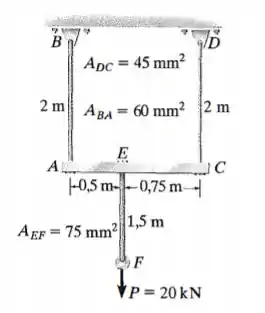
O conjunto é composto por três hastes de titânio e uma barra rígida . A área da seção transversal de cada haste é dada na figura. Se uma força vertical for aplicada ao anel , determine o deslocamento vertical do ponto . .
Passo 1
Oláaaa, querido! Tá bem?
Então, temos uma barra rígida sendo suportada por duas hastes. E nessa barra rígida temos uma haste, e a puxando para baixo temos uma força de .
Aí ele quer saber qual é o deslocamento do ponto quando essa força é aplicada. Esse ponto se desloca porque as hastes vão ser deformadas por causa da carga, elas vão se alongar.
Falou de alogamento por causa de uma carga, você lembra dessa fórmulinha:
Vamos usar ela nas nossas barras e um pouco de geometria para saber o deslocamento do ponto . Bora ver como!
Passo 2
Para aplicar aquela fórmulinha nas nossas barras, precisamos achar as forças normais internas nas barras.
Percebe que a barra está sendo diretamente puxada pela força de , então podemos dizer que
Agora precisamos achar as forças internas para as outras barras. Para isso, vamos aplicar as equações da estática à nossa barra :
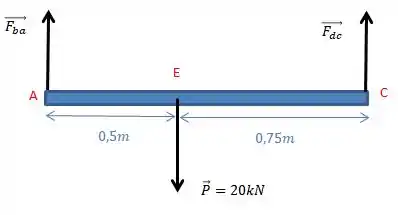
Calculando o momento em relação ao ponto A, tomando o sentido anti-horário como positivo:
Avaliando a segunda lei de newton, para as forças em y:
Passo 3
Calculadas as forças acima, podemos encontrar as deformações em cada barra, que servirão de base para que possamos encontrar o deslocamento em . Assim, aplicando a fórmula descrita no primeiro passo vamos ter
Aplicando primeiro para a barra DC. Vamos achar o quando essa barra é alongada, e assim o quanto o ponto se move para baixo, já que o ponto é fixo:
Analogamente para a barra , onde o ponto A é o que vai sofrer o deslocamento:
Achando também o alongamento da barra :
Passo 4
Então, a gente quer saber o deslocamento total do ponto , certo?
Uma parte desse deslocamento vai ser o alongamento da barra que a gente achou .
E a outra parte acontece porque a barra rígida desce um pouco porque os seus suportes, as barras e , sofrem alongamento. E assim, o ponto , que está na barra rígida, vai descer um valor, que vamos achar de .
Aí a gente pode dizer que o deslocamento de é a soma do deslocamento de e do alongamento de :
Só que não temos ainda.
Passo 5
Bem, dado pela geometria da figura. Como as barras e não se deformam igualmente, a barra rígida vai ficar um pouco inclinada, então a gente vai precisar olhar a geometria da deformação com mais carinho para saber o quando desceu:
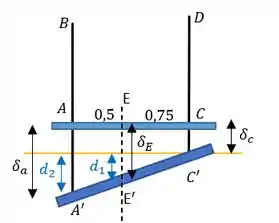
Vê que o alongamento de é menor que o alongamento de . E que o alongamento dessas barras é igual ao valor que a extremidade inferior delas vai ser mover.
Com isso a gente pode fazer uma semelhança de triângulos e achar o deslocamento do ponto da seguinte forma:
Passo 6
Por fim, deslocamento exatamente no ponto será dada por