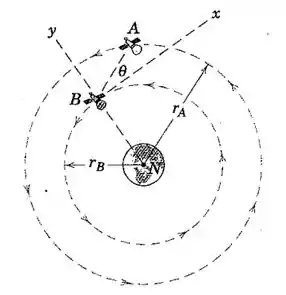
Dois satélites estão em orbitas circulares equatoriais de diferentes altitudes. O satélite A está em uma órbita geossíncrona (uma com o mesmo período que o da rotação da Terra, de modo que ele “paira” sobre o mesmo ponto no equador). O satélite B possui uma órbita de raio Calcule a velocidade que A aparenta ter para um observador fixo em B quando o ângulo de elevação é igual a (a) Os eixos x-y esrão presos em B, cuja antena sempre aponta para o centro da Terra (direção y). Consulte a Seção 3/13 e o apêndice D para as informações necessárias sobre as órbitas.
Passo 1
Bom pessoal, vamos buscar na Seção 3/13 e o apêndice D/2 as informações necessárias para a resolução do problema.
Uma órbita circular pode ser encontrada a partir da relação:
Juntando essa equação de cima com , podemos calcular o raio de órbita de A:
E também podemos calcular as velocidades de A e B por esta equação:
Podemos ainda calcular a velocidade angular de B por:
Passo 2
- Nesta condição, Então temos o seguinte:
- Nesta condição, Então temos o seguinte:
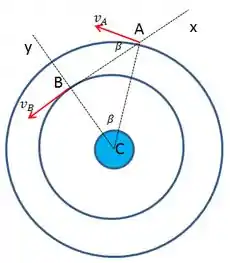
Pelo triangulo retângulo formado ABC, podemos calcular o ângulo e a distancia
Agora usamos a equação da velocidade relativa:
Passo 3
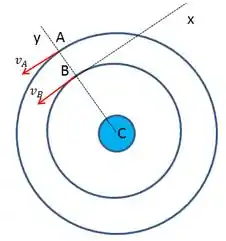
Logo
Agora usamos a equação da velocidade relativa: