Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 82
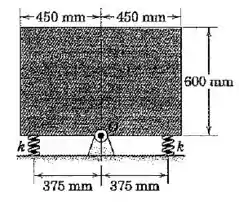
O bloco retangular homogêneo de é articulado em torno de um eixo horizontal que atravessa e é apoiado por duas molas, cada uma de rigidez . A base do bloco está horizontal na posição de equilíbrio, com cada mola sob uma força compressiva de . Determine a rigidez mínima das molas, que garantirá vibração em torno da posição de equilíbrio.
Passo 1
Vamos começar com uma equação de momentos em relação ao ponto :
O momento da força peso vai seguir a relação usual. Nesse caso, o centro de massa está a uma distância do ponto, então:
Mas ao contrário do que costuma acontecer, dessa vez o momento da força peso tem sinal positiva, porque ele contribui para o aumento do deslocamento angular .
Já para o momento das forças nas molas, temos que analisar o seguinte:
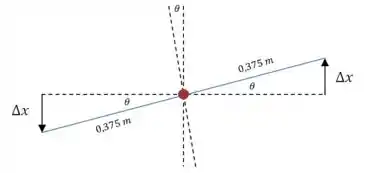
Então as forças nas molas terão o seguinte módulo:
E a distância perpendicular de cada uma delas até o ponto é:
Então (como temos duas molas):
Beleza, já podemos escrever uma expressão para o somatório do lado esquerdo da equação:
Passo 2
Agora vamos substituir isso na nossa equação principal:
E fazer as aproximações e :
O objetivo da questão é mostrar um valor de que garanta que haja vibração em torno da posição de equilíbrio.
Para garantir isso, precisamos de um valor de para o qual a última equação que escrevemos seja a equação de um oscilador harmônico. Nesse caso:
A única exigência para isso é que o termo do lado direito seja positivo. Então, no caso limite:
Resposta
A mola deve ter uma rigidez mínima de .