Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 180

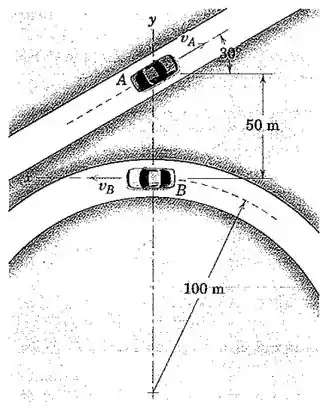
Cada um dos dois carros A e B está viajando com uma velocidade constante de 72 km/h. Determine a velocidade e a aceleração do carro A como percebida por um observador se deslocando e girando com o carro B quando estão nas posições mostradas. Os eixos x-y estão presos no carro B. Esboce ambos os vetores do movimento relativo.

Passo 1

Bom pessoal, a primeira coisa que vamos fazer é calcular as velocidades. O carro A está se deslocando com velocidade constante em uma direção de 30 graus com a horizontal. O carro B percorre uma trajetória circular e neste instante sua velocidade está na direção horizontal. Podemos calcular, então, a velocidade angular de B:

ω = - v B r = - 72 3,6 × 100 = - 0,2 k ^   r a d / s

Reparem no sentido do eixo x na figura para não errar o sinal!!

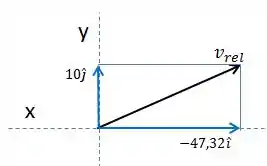
Vamos usar agora o conceito de velocidade relativa:

v A = v B + ω × r A B + v r e l

Substituindo os valores:

20 - c o s 30   i ^ + s e n 30   j ^ = 20 i ^ - 0,2 k ^ × 50 j ^ + v r e l

v r e l = - 47,32 i ^ + 10 j ^ m s

Representando o esboço:

Passo 2

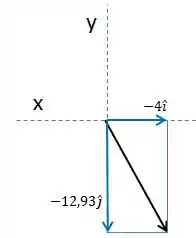
Agora, vamos para o cálculo das acelerações.

O carro A faz uma trajetória linear e possui velocidade constante. Logo não possui aceleração a A = 0 .

Já o carro B percorre uma trajetória circular, tendo então uma componente normal:

a B = - r ω 2 = - 100 j ^ - 0,2 2 = - 4 j ^   m / s 2

Agora, vamos usar a equação da aceleração relativa entre os pontos A e B.

a A = a B + α × r A B + ω × ω × r A B + 2 ω × v r e l + a r e l

Substituindo os valores:

0 = - 4 j ^ + 0 - - 0,2 2 50 j ^ + 2 - 0,2 k ^ × - 47,32 i ^ + 10 j ^ + a r e l

0 = - 4 j ^ - 2 j ^ + 18,93 j ^ + 4 i ^ + a r e l

a r e l = - 4 i ^ - 12,93 j ^   m / s 2

Representando graficamente:

Resposta

v r e l = - 47,32 i ^ + 10 j ^ m s

a r e l = - 4 i ^ - 12,93 j ^ m s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, o tubo gira em torno do eixo z com uma velocidade angular constante ω 1 = 2r a d / s , enquanto no mesmo instante o tubo gira para cima a uma taxa constante ω 2 = 5r a d / s . Se
No instante mostrado, a base do braço robótico gira em torno do eixo z com uma velocidade angular ω 1 = 4 r a d / s , a qual está aumentando a ω ˙ 1 = 3r a d / s 2 . Além disso, a lança B C gira com u
Se o anel A se desloca com uma velocidade constante v A = 5 im / s , determine a velocidade do anel B quando a barra A B está na posição mostrada. Suponha que a velocidade angular de A B é perpendicul
No instante mostrado, o tubo gira em torno do eixo z com uma velocidade angular xonstante ω 1 = 2r a d / s , enquanto no mesmo instante o tubo gira para cima com uma taxaconstante de ω 2 = 5r a d / s
No instante θ = 30 ° , a estrutura do guindaste e a lança A B está girando com uma velocidade angular constante ω 1 = 1,5r a d / s e aceleração angular ω ˙ 1 = 0,5r a d / s 2 , equanto a lança A B gir