Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 185
Determine a aceleração angular da haste EC na posição mostrada, onde quando O pino A é fixo na haste EC. A ranhura circular no elemento DO tem um raio de curvatura de 150 mm. Na posição mostrada, a tangente à ranhura no ponto de contato é paralela a AO.
Passo 1
Bom pessoal, novamente temos um componente ranhurado, então pegamos um ponto P coincidente a A, mas que pertence a DO. Muito importante também destacar que a tangente à ranhura em A é paralela a AO. Vamos fazer um esboço do mecanismo com os dados para visualizar melhor.
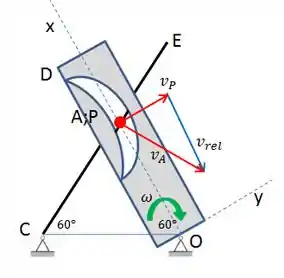
Vamos observar os vetores velocidade. O ponto A pertence à haste CE, então sua velocidade é perpendicular à mesma. Da mesma forma, o ponto P pertence ao componente DO, então sua velocidade é perpendicular à DO. Já a velocidade relativa deve ter a direção da ranhura, que o enunciado diz que é paralelo a DO. Vejamos o diagrama dos vetores velocidade:
Podemos calcular a velocidade do ponto P a partir do componente DO:
E pela relação dos vetores, podemos calcular as outras velocidades:
Passo 2
Agora, vamos para o cálculo das acelerações.
Vamos usar a equação da aceleração relativa entre os pontos A e O:
Beleza! Agora vamos usar os conceitos dos vetores acelerações que aparecem na equação acima para fazer um esboço e calcular os valores. A aceleração de A em relação à haste CE possui uma componente normal e uma tangencial. Da mesma forma, a aceleração relativa também possui estas componentes, porém em relação à ranhura. Com isso, podemos fazer o diagrama das acelerações:
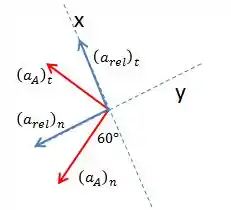
OBS: não tem problema caso o sentido dos vetores da figura estiverem errado, isso iremos descobrir através dos cálculos. Vamos lá.
A aceleração de A pode ser calculada também a partir da haste CE. Atenção aos eixos x-y:
A aceleração relativa normal pode ser calculada por:
Agora sim, vamos substituir os valores na equação da aceleração relativa entre A e O:
Decompondo nas direções:
Resolvendo o sistema, temos que: