Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 186

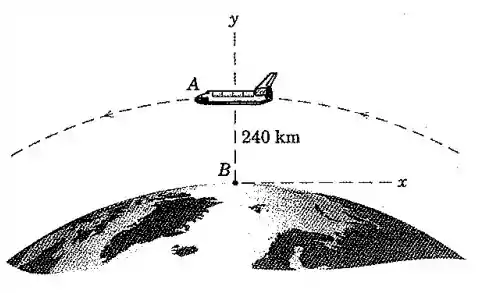
O ônibus espacial A está em uma órbita circular equatorial de 240 km de altitude e está se movendo de oeste para leste. Determine a velocidade e a aceleração que ele parece ter para um observador B fixo no equador e girando com a Terra enquanto o onivus espacial apssa acima de sua cabeça. Use R=6378 km para o raio da Terra. Use também a Fig. 1/1 para o valor apropriado de g e faça seus cálculos para uma precisão de quatro algarismos significativos.

Passo 1

Bom pessoal, vamos buscar as informações necessárias para a resolução do problema.

R = 6378   k m

g = 9,814   m / s 2

ω T = 7,292 × 10 - 5 r a d / s

Uma órbita circular pode ser encontrada a partir da relação:

v = R g r  

Desta forma, a velocidade de A pode ser calculada por:

v A = R g R + 240 = 6378 9,814 1000 ( 6378 + 240 ) = 7,77 k m s = 27960 k m h ←

A velocidade do observador B pode ser calculada como sendo a da Terra:

v B = ω T × R = 7,292 × 10 - 5 k ^ × 6378 j ^ = 0,465 k m s = - 1674   i ^   k m / h

Para encontrar a velocidade relativa, vamos aplicar a equação:

v A = v B + ω × r A B + v r e l

- 27960 i ^ = - 1674 i ^ + 7,292 × 10 - 5 k ^ × 240 j ^ + v r e l

v r e l = - 26220   i ^ k m h

Passo 2

Agora vamos para o cálculo da aceleração. Usando a equação da aceleração relativa:

a A = a B + α × r - r ω 2 + 2 ω × v r e l + a r e l

A aceleração de A pode ser calculada a partir da sua componente normal:

a A = - v A 2 R + 240 = - 27960 3,6 2 1000 6378 + 240 = - 9,115 j ^ m s 2 ↓  

Da mesma forma, encontramos a aceleração de B:

a B = R ω 2 = - 6378000 7,292 × 10 - 5 2 = - 0,0339 j ^ m s 2

Substituindo os valores:

- 9,115 j ^ = - 0,0339 j ^ + 0 - 240000 j ^ 7,292 × 10 - 5 2 + 2 7,292 × 10 - 5 k ^ × - 26220   i ^ 3,6 + a r e l

- 9,115 j ^ = - 0,0339 j ^ - 0,001276 j ^ - 1,0622 j ^ + a r e l

a r e l = - 8,018   m / s 2

Resposta

v r e l = - 26220   i ^ k m h

a r e l = - 8,018 j ^   m s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, a estrutura da escavadeira se desloca para frente na direção y com uma velocidade de 2m / s e uma aceleração de 1m / s 2 , enquanto a cabine gira em torno do eixo z com uma veloc
No instante quando θ = 90 ° , o corpo do satélite se desloca na direção x com uma velocidade v O = 500 im / s e aceleração a o = 50 i m / s 2 . Simultaneamente, o corpo também gira com uma velocidade
O cone rola em um círculo e gira em torno do eixo z a uma taxa constante ω z = 8r a d / s . Determine a velocidade e a aceleração angular do cone se ela rola sem deslizar. Além disso, qual é a velocid
No instante quando θ = 90 ° , o corpo do satélite está girando com uma velocidade angular ω 1 = 15r a d / s e aceleração angular ω ˙ 1 = 3r a d / s 2 . Simultaneamente, os painéis solares giram com um
Se a estrutura gira com uma velocidade angular constante ω p = - 10 kr a d / s e a engrenagem horizontal B gira com uma velocidade angular constante ω B = 5 kr a d / s , determine a velocidade angular