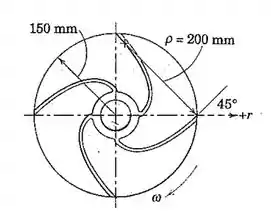
A figura mostra as pás do impelidor de uma bomba centrífuga que gira com uma velocidade constante no sentido horário de 200 rpm. As partículas de fluido possuem uma velocidade absoluta cuja componente na direção r é de 3 m/s na descarga da palheta. Além disso, o módulo da velocidade das partículas medido em relação à palheta está aumentando na taxa de 24 m/s² antes de saírem da palheta. Determine o modulo da aceleração total de uma partícula de fluido imediatamente antes de sair do impelidor. O raio de curvatura da palheta em sua extremidade é de 200 mm.

Pessoal, vamos fazer um esboço do sistema supondo uma partícula A na ponta da Palheta P. Pelo enunciado, sua velocidade na componente r .

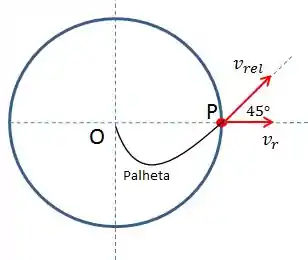
Pela figura, vemos que a partícula de fluido sai a uma direção de 45 graus com r. Desta forma, podemos calcular

A aceleração da partícula pode ser descrita em relação à da palheta P:

Como a partícula A é coincidente a ponta da palheta P neste instante, então A equação então fica:

A aceleração da palheta P possui apenas componente normal em relação ao centro O:

O módulo da aceleração relativa da partícula em relação à curvatura da palheta é dado no enunciado, sendo . Podemos fazer um novo diagrama com as acelerações para melhor visualização:

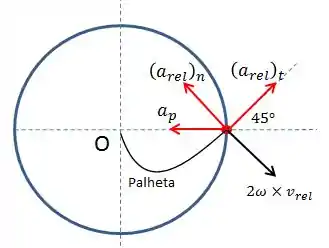
Podemos também calcular a aceleração normal em relação à curvatura da palheta:

Agora vamos substituir os valores na equação da aceleração relativa. Mas vamos usar as componentes , sendo necessário passar para estas direções.

Como é pedido o módulo da aceleração: