Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 140

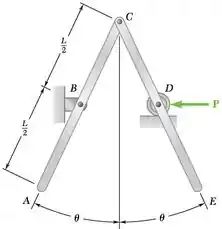
Duas barras idênticas AC e CE, cada uma com peso W, são ligadas em forma de articulação como mostrado na figura. Sabendo que no instante mostrado a força P faz com que o rolo ligado a D se mova para a direita com velocidade constante vD, determine a intensidade da força P em termos de L, W, vD e θ .

Passo 1

Cinemática: Velocidade:

O componente horizontal de vC é igual a vD/Z ←

v C cos ⁡ θ = 1 2 v D

v C = v D 2 cos ⁡ θ     θ

Passo 2

Haste AC:

v C = L 2 ω A C

v D 2 cos ⁡ θ = L 2 ω A C

ω A C = v D L cos ⁡ θ

Passo 3

Por simetria:

ω C D = ω A C

Além disso, como aD = 0, a componente horizontal de aC é zero. Assim, aC é vertical

Aceleração: Haste AC

a C t = a C n tan ⁡ θ

L 2 α A C = L 2 ω A C 2 tan ⁡ θ

α A C = ω A C 2 tan ⁡ θ = v D L cos ⁡ θ 2 tan ⁡ θ = v D 2 L 2 tan ⁡ θ cos 2   θ  

Passo 4

Por simetria:

α A C = α C D

α C E = v D 2 L 2 tan ⁡ θ cos 2 θ

Cinética: Sistema inteiro

→ + Σ M B = → + Σ M B eff:             W - D y B D = I - α C E - α A C

Desde

α C G = α A C ,               n ó s   a c h a m o s               D y = W ↑

Passo 5

Cinética: Haste CE

+ Σ M C = Σ M C eff:             P L 2 cos ⁡ θ = - I - α C E

P L 2 cos ⁡ θ = m 12 L 2 v D 2 L 2 ∙ tan ⁡ θ cos 2   θ

Resposta

P = m v D 2 6 L ∙ tan ⁡ θ cos 3   θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma haste esguia e uniforme de comprimento l e massa m gira em torno de um eixo vertical AA 'com velocidade angular constante ω . Determine a tensão na haste a uma distância x do eixo de rotação.
Uma haste fina e uniforme de comprimento L = 900 mm e massa em = 4 kg é suspensa de uma dobradiça em C. Uma força horizontal P de magnitude 75 N é aplicada na extremidade B. Sabendo que r = 225 mm, de
Um disco de turbina de massa 26 kg gira a uma taxa constante de9.600 rpm. Sabendo que o centro de massa do disco coincide com ocentro de rotação O, determine a reação em O imediatamente depoisque uma
No Problema 16.78, determine (a) a distância r para a qual o componente horizontal da reação em C é zero, (b) a aceleração angular correspondente da barra.
Um grande volante é montado em um eixo horizontal e gira a uma taxa constante de 1200 rpm. Dados experimentais indicam que a força total exercida pelo volante no eixo varia de 55 kN para cima a 85 kN