Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 112

Uma pequena colua de 120 mm × 180 mm suporta três cargas axiais mostradas. Sabendo-se que a seção ABD é suficientemente afastada das cargas, para que permaneça plana, determinar a tensão no: (a) canto A; (b) canto B.

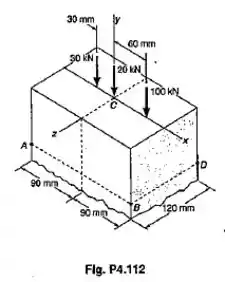
Passo 1

Teremos para área superior

A = 0,12 × 0,18 = 0,216   m 2

Somatório de momentos (anti horário positivo)

M c = - 30 × 30 + 60 × 100 = 5,1   k N . m

Para o momento de inércia

I = b × h 3 12 = 0,12 × 0,18 3 12 = 5,832 × 10 - 5   m 4

Por último mas certamente não menos importante temos o σ 1

σ 1 = - 30 × 10 3 + 20 × 10 3 + 100 × 10 3 0,0216 = - 150 × 10 3 0,0216 = - 6,944   M P a

Passo 2

Com isso já podemos comçar a calcular o que cada letra pede! Para a letra a o σ A T O T A L será dao por

σ A T O T A L = M c I = 5,1 × 10 3 × 0,09 5,832 × 10 - 5 - 6,944 × 10 6 = 7,87 - 6,944 × 10 6 = 926   k P a

Passo 3

Por último, para a letra (b) vamos ter simplesmente um sinal invertindo já que estamos agora trabalhando na outra ponta.

σ B T O T A L = - 7,87 - 6,944 × 10 6 = - 14,814   M P a

Resposta

a ) σ A t o t a l = 926   k P a

b )   σ B t o t a l = - 14,814   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A travessa ou longarina de suporte principal da carroceda do caminhão está sujeita à carga distribuída uniforme. Determine a tensão de flexão nos pontos A e B .
Uma porção de fêmur pode ser modelada como um tubo com diâmetro interno de 9,5m m e diâmetro externo de 32m m . Determine a força estática elástica máxima P que pode ser aplicada ao centro do osso sem
Determine o menor diâmetro admissível para o eixo que está sujeito às forças concentradas. Os mancais de luva em A e B suportam somente forças verticais, e a tensão de flexão admissível é σ a d m = 15
Determine a tensão de flexão máxima absoluta no eixo de 30 m m de diâmetro que está sujeito às forças concentradas. Os mancais de luva em A e B suportam somente forças verticais.
Determine o menor diâmetro admissível do eixo que está sujeita às forças concentradas. Os mancais de luva em A eB suportam somente forças verticais, e a tensão de flexão admissível é σ =160M P a .