Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 127
As duas forças que atuam nos cabos das chaves de grifo formam um binário . Expresse o binário como um vetor.
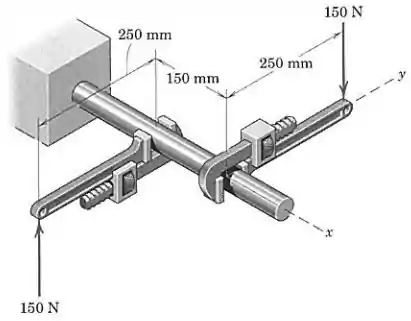
Passo 1
Note que, na direção , a distância entre as duas forças é . Como as forças ocorrem na direção , o momento em relação ao eixo é:
Analogamente, temos:
As forças não produzem momento em relação ao eixo :
Logo,
Resposta
Exercícios de Livros Relacionados
A chave especial mostrada é usada para parafusos de difícil acesso que tem uma especificação de baixo torque. Determine o momento da força de 40N aplicada no ponto A do cabo da chave em relação a O .
Para reduzir o momento indesejável em relação ao eixo x , um mecânico usa sua mão esquerda para sustentar o cabo da chave no ponto B . Que força direcionada para cima, F , deve ser exercida para que n
O momento M → aplicado à polia causa uma força trativa T = 80N no cabo, que está preso à polia em D e ao chão em E . Determine o momento em relação a O dessa força de 80N , quando aplicada em C .
Determine o momento da força de 400N em relação ao ponto A (a) usando a relação do produto vetorial e (b) projetando a força em seus componentes e achando seus respectivos momentos.
A chave especial mostrada na figura é projetada para ter acesso ao parafuso de segurança de alguns distribuidores de automóvel. Para a configuração mostrada, onde a chave está em um plano vertical e u