Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 137
O momento aplicado à polia causa uma força trativa no cabo, que está preso à polia em e ao chão em . Determine o momento em relação a dessa força de , quando aplicada em .
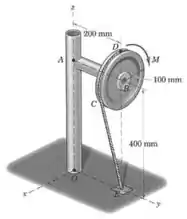
Passo 1
Vamos começar desenhando os vetores e :
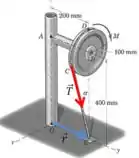
O vetor pode ser escrito logo de cara:
E para escrever o vetor precisamos escrever o vetor unitário na direção do cabo . Podemos fazer isso baseados no ângulo :
E podemos calcular usando a seguinte relação:
E então:
Passo 2
E agora podemos calcular o momento fazendo o produto vetorial:
E vamos usar a regra da mão direita para determinar os produtos vetoriais:
E então:
Então o momento total é:
Resposta
O momento total em relação a é .
Exercícios de Livros Relacionados
O estrado da empilhadeira da máquina do Prob 4/98 está mostrado com detalhes dimensionais adicionais. Determine a força no cilindro hidráulico único, C D . A massa do cubo de tijolos é de 2000 kg, com
Calcule a força na conexão A B das garras de elevação que se cruzam sem se tocar.
Os elementos de um mecanismo acionados por uma mola, da tampa do porta-malas de um carro, estão mostrados na figura. Para a posição de equilíbrio mostrada, determine o momento M A que cada uma das mol
Determine a força de aperto vertical em E em termos da força P aplicada ao cabo do rebitador.
A morsa com dois atuadores mostrada na figura é usada para dar uma força de aperto adicional quando os parafusos são apertados. Se o parafuso vertical é apertado para produzir uma força de aperto de 3