Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 65
As duas forças e que atuam em possuem uma força resultante . Determine a intensidade e os ângulos de direção coordenados de .
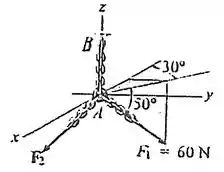
Passo 1
Queremos encontrar a já tendo e , vamos começar decompondo essa última:
De início já podemos encontrar a direção , dado que a força faz com o plano :
Já, a projeção no plano é dada por:
E então podemos decompor em e :
Temos em
E temos em :
E o vetor cartesiano de fica:
Repare que o sinal da direção e é negativo devido o sentido da força representado na imagem.
Passo 2
Agora vamos igualar o somatório das forças a nossa :
E a intensidade de em módulo será:
Passo 3
Por último, achamos seus ângulos de direção coordenados:
Então:
Resposta
Exercícios de Livros Relacionados
Uma força atua na origem de um sistema de coordenadas na direção definida pelos ângulos θ y = 55 ° e θ z = 45 ° . Sabendo que a componente x da força é -2220N, determine, ( a ) o ângulo θ x , ( b ) os
Sabendo que a tração no cabo AC é 2130 N, determine a componente da força exercida na placa em C.
Determine ( a ) as componentes x ,y e z da força de 750 N, ( b ) os ângulos θ x , θ y e θ z que a força forma com os eixos coordenados.
Uma torre de transmissão é sustentada por três cabos de sustentação ancorados por parafusos em B, C e D. Se a tração no cabo AB é 2335 N determine os componentes da força exercida pelo cabo no parafus
Para a barra de aço e o cabo do Problema 2.87, determine os componentes da força exercida pelo cabo no suporte em E.