Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 68
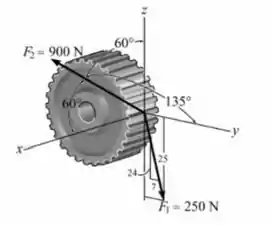
A engrenagem está submetida às duas forças caudadas pelo contato com outras engrenagens. Determine a resultante das duas forças e expresse o resultado como um vetor cartesiano.
Passo 1
Fala ai galerinha do RespondeAi, tudo beleza?
O exercício pede pra gente expressar a força resultante como um vetor cartesiano, pra isso vamos primeiro decompor as forças e e somar suas componentes. Bora lá!
A está no plano então teremos duas componentes e encontraremos pela relação de catetos e hipotenusas do triângulo dado, tal que:
E no eixo :
Sendo assim, o vetor cartesiano de fica:
Nossa direção é negativa de acordo com o sentido negativo da força em .
Passo 2
Já para nossa força são dados dois ângulos de direção coordenados, vamos encontrar o terceiro pela relação:
Assim:
Logo, como a força está no sentido positivo do eixo , teremos , de modo que:
Passo 3
Agora podemos somar as forças e suas componentes pra poder encontrar a resultante , tal que:
Portanto:
