Determine a menor força que causará a iminência de movimento. A caixa e a roda têm uma massa de e , respectivamente. O coeficiente de atrito estático entre a caixa e o piso é , e entre a roda e o piso é .
Passo 1
O problema pede que descubra a menor força horizontal para que ocorra movimento.
Bom galera, pra facilitar a gente começa fazendo um diagrama de corpo livre na caixa.
E a gente sabe que o peso da caixa é dada por:
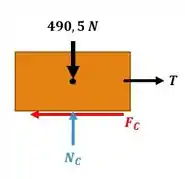
A gente vai precisar calcular a força tração necessária para vencer o atrito e começar o movimento da caixa.
Passo 2
Se a gente olha o eixo vertical só tem a normal e o peso atuando, então elas são iguais:
Assim o atrito estático máximo é:
Então para a caixa entrar em movimento ela precisa vencer a força de atrito, então:
Passo 3
Beleza, então vamos encontrar a força , pra isso a gente vai analisar as forças atuantes na roda, pra isso vamos fazer mais um diagraminha:
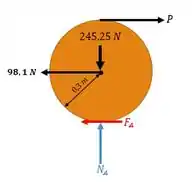
Vamos começar com o que a gente já tem quase que dado pra gente, que é a normal que vai anular a peso, então:
E o atrito também é fácil de calcular:
Então, para a roda não derrapar não pode ultrapassar .
Passo 4
Vamos calcular o momento, tendo como eixo de rotação o ponto da roda que tá encostada no chão:
Assim, encontramos:
Vamos só testar se a roda vai derrapar:
Então a roda não derrapa, assim a força necessaria para movimento é: