Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 22
Para a treliça de aço e os carregamentos mostrados, determine as deformações dos componentes BD e DE, sabendo que suas áreas de seção transversal são, respectivamente, e
Passo 1
E ai gurizada tudo bem?? Antes de mais nada vamos desenhar o diagrama de corpo livre para facilitar os cálculos, então vem comigo !!!
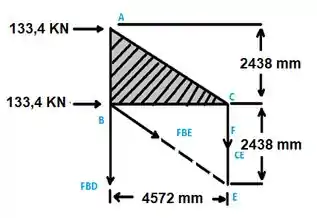
Vamos começar calculando o somatório do momento em E temos...
Passo 2
Agora gurizada considerando a segunda parte da treliça temos que desenhar novamente o diagrama de corpo livre ...
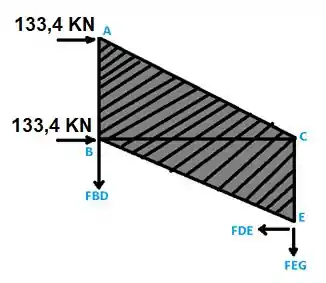
Calculando o somatório das forças em x...
Calculando a deformação na seção BD temos...
Agora para a seção DE temos...
Resposta
Exercícios de Livros Relacionados
As deformações abaixo foram determinadas na superfície da base de uma máquina de ferro fundido. Sabendo-se que E = 70 G P a e G = 28 G P a , determinar os planos principais e as tensões principais: (a
As seguintes leituras foram obtidas, com uma roseta de deformação colada à superfície de um comonente de máquina: ε 2 = - 90 × 10 - 6m m / m m ε 3 = - 190 × 10 - 6m m / m m ε 4 = - 240 × 10 - 6m m / m
Um quadrado A B C D de 15m m de lado é riscado sobre a superfície de uma placa fina, quando a placa está sem carga. Depois da placa ser carregada, observou-se que o comprimento do lado A B diminui em
As seguintes leituras foram obtidas, com uma roseta de deformação colada à superfície de um comonente de máquina: ε 1 = - 57,5 × 10 - 6m m / m m ε 2 = - 57,5 × 10 - 6m m / m m ε 4 = + 2 20 × 10 - 6m m
As deformações específicas normais determinadas com o uso da roseta da figura, colada na superfície de um componente estrutural, são: ε 1 = - 57,5 × 10 - 6m m / m m ε 2 = - 57,5 × 10 - 6m m / m m ε 4