Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas de Revisão - Ex. 70
As duas partes do elemento AB são coladas ao longo de um plano formando um ângulo com a horizontal. Sabendo que o limite de tensão para a junta colada é de 17,2 MPa em tração e de 9 MPa em cisalhamento, determine o intervalo de valores de para o qual o coeficiente de segurança dos elementos seja pelo menor 3,0.
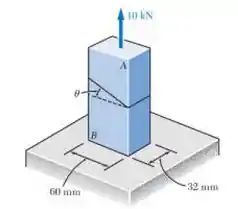
Passo 1
E ai gurizada tudo belezinha? Primeiramente vamos calcular a área da base do elemento:
Sendo:
Com base na tensão de tração, temos:
Passo 2
Com base na tensão de cisalhamento,
Resposta
Exercícios de Livros Relacionados
Resolver o Prob. 162, assumindo que 25k W é absorvido em cada engrenagem.
Determinar a carga uniformemente distribuída admissível w , para a viga mostrada, sabendo-se que σ a d m = + 70M P a na tração, σ a d m = - 130M P a , na compressão, e que τ a d m = 60M P a .
Uma barra de aço uniforme de diâmetro d é içada por cabos de um guindaste, amarrados em A e B . Pede-se: (a) determinar a distância a , entre as extremidades da barra e os pontos onde os cabos estão a
Sabendo-se que τ a d m = 50M P a , determinar o menor diâmetro permissível para o eixo maciço A B , quando P = 2N , l = 30 0m m e L = 75m m . Incluir o efeito das tensões de cisalhamento, causadas pel
Usando a notação da Sec. 7.9 e desprezando o efeito das tensões de cisalhamento, causadas por cargas transversais; mostrar que a máxima tensão normal, em um eixo circular, pode ser expresso como segue