Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 11

As duas pequenas esferas, cada uma com massa m , estão rigidamente conectadas por uma haste de massa desprezível. O centro C da haste possui uma velocidade v na direção x , e a haste está girando no sentido anti-horário na taxa constante θ ˙ . Para um dado valor de θ , escreva as expressões para

(a) a quantidade de movimento linear de cada esfera e

(b) a quantidade de movimento linear G do sistema de duas esferas.

Passo 1

(a) As duas esferas realizam um movimento circular em torno do centro C da haste, com velocidade perpendicular à haste de módulo r θ ˙ = b θ ˙ . Além disso, ambas têm velocidade v para a direita, acompanhando o movimento da haste.

Os vetores dessas velocidades estão representados na figura a seguir:

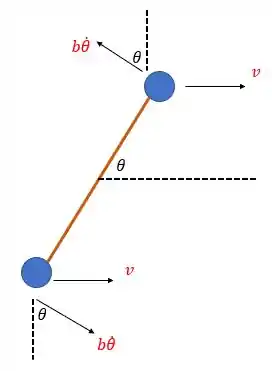
Portanto, se decompormos as velocidades (em vermelho) nos eixos x e y , obtemos a quantidade de movimento linear de cada esfera. Para a esfera 1 (mais baixa), temos:

G 1 = m   v   i + b θ ˙   s e n   θ   i - b θ ˙ cos ⁡ θ j

G 1 = m   v + b θ ˙   s e n   θ   i - b θ ˙ cos ⁡ θ j

E para a esfera 2 (mais alta), temos:

G 2 =   m   v   i - b θ ˙   s e n   θ   i + b θ ˙ cos ⁡ θ j

G 2 = m   v - b θ ˙   s e n   θ   i + b θ ˙ cos ⁡ θ j

Passo 2

(b) Para calcular a quantidade de movimento linear do sistema, basta somar as quantidades individuais de cada esfera, já calculadas no item anterior:

G = G 1 + G 2

G = m   v + b θ ˙   s e n   θ   i - b θ ˙ cos ⁡ θ j + m   v - b θ ˙   s e n   θ   i + b θ ˙ cos ⁡ θ j

G = m   v + b θ ˙   s e n   θ + v - b θ ˙   s e n   θ   i + - b θ ˙ cos ⁡ θ + b θ ˙ cos ⁡ θ   j

G = m   2 v   i

G = 2 m v   i

Resposta

(a) G 1 = m   v + b θ ˙   s e n   θ   i - b θ ˙ cos ⁡ θ j

G 2 = m   v - b θ ˙   s e n   θ   i + b θ ˙ cos ⁡ θ j

(b) G = 2 m v   i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um piloto de 54 kg pilota um jato de treinamento em um meio “loop” de 1.200 m de raio de modo que a velocidade escalar do jato diminui a uma taxa constante. Sabendo que o peso aparente do piloto no po
Um bloco B de 250 g se encaixa dentro de uma pequena cavidade aberta no braço OA, que gira no plano vertical a uma taxa constante tal que v = 3 m/s. Sabendo que a mola exerce no bloco B uma força de i
A curva em um circuito de velocidade tem raio de 300 m e velocidade de segurança de 192 km/h. (Ver no Problema Resolvido 12.5 para a definição da velocidade de segurança.) Sabendo que o carro de corri
Um automóvel de 1.200k g está movendo a uma velocidade 90k m / h quando os freios são totalmente aplicados, causando o escorregamento de todas as quatro rodas. Determine o tempo necessário para parar
Um colar de 2 kg pode deslizar sobre uma barra vertical sem atrito e está sujeito a uma força P cuja intensidade varia como mostrado na figura. Sabendo que o colar está inicialmente em repouso, determ