Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 151

A roda dupla de 10   k g , com raio de giração de 125   m m em relação a O , está ligada à mola de rigidez k = 600 N / m por um fio que está enrolado firmemente em torno do eixo central. Se a roda é liberada a partir do repouso no plano inclinado com a mola esticada em 225   m m , calcule a velocidade máxima v do seu centro O durante o movimento que se segue. A roda rola sem deslizar.

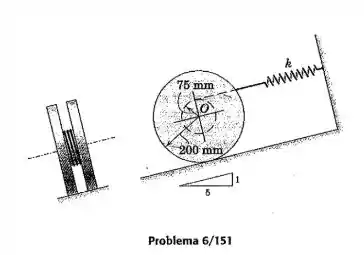
Passo 1

Seja x a distância percorrida pelo ponto O, localizado no centro da roda e θ a inclinação do plano.

θ =   t g - 1 1 5 = 11,31 °

A variação da energia potencial gravitacional é dada por

∆ V g = m g x s e n θ = 10 9,81 0,1961 x = 19,24 x

A variação da energia potencial elástica, por sua vez, é dada por

∆ V e = 1 2 k x 2 2 - x 1 2 = 1 2 600 0,225 - 275 200 x 2 - ( 0,225 ) ²

Resolvendo a equação anterior chegamos na seguinte expressão

∆ V e = 567,1875 x 2 - 185,625 x

Por fim, para a variação da energia cinética

∆ T = 1 2 m v + 1 2 I - ω 2       →         ∆ T = 1 2 10 v 2 + 1 2 ( 10 ) ( 0,125 ) ² v 0,2 2

Simplificando, chegamos em

∆ T = 6,95 v ²

Passo 2

Sabemos que, para o sistema,

U ' = ∆ T + ∆ V g + ∆ V e

Substituindo os valores obtidos nos passos anteriores, ficamos com

0 =   6,95 v 2 +   19,24 x + 567,1875 x 2 - 185,625 x

Agrupando,

v 2 = - 81,57 x ² + 23,93 x

Para acharmos v m á x , derivamos e igualamos a zero a equação anterior. Para d d t v 2 = 0 , temos

0 =   - 163,14 x + 23 ,   93         →           x = 0,1467   m  

Ou seja, para x = 0,1467   m   temos v m á x .

v m á x =   - 81,57 0,1467 2 + 23,93 ( 0,1467 ) 2

De onde obtemos

v m á x = 1,3249 m s

Resposta

v m á x = 1,3249 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma corda com massa total 0,4k g e comprimento total 4m tem 0,6m de seu comprimento pendente para fora de uma bancada de trabalho. Qual será o trabalho necessário para colocar toda a corda sobre a ban
Uma criança desliza um bloco de massa 2k g ao longo de um piso de cozinha liso. Se a velocidade inicial é 4m / s e o bloco bate em uma mola com constante de mola 6N / m , qual será a conrpressão máxim
Uma bola extremamente elástica de massa M e um bloco de mármore de massa m são liberados em queda de uma altura h com o bloco de mármore logo acima da bola. Uma bola desse tipo apresenta um coeficient
Efetue um cálculo no computador para um objeto se movimentando verticalmente no ar sob a ação da gravidade e sujeito a uma força de retardo proporcional ao quadrado da velocidade do objeto (veja a Equ
Um trem se move ao longo da via em velocidade constante u. Uma mulher no trem arremessa uma bola de massa m em linha reta para frente, com velocidade v em relação a ela mesma.Qual é o ganho de energia