Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 16
Duas placas de aço de 12 x 220 mm de seção transversal retangular são soldadas a um perfil W250 x 58 como mostra a figura. Determine a maior força cortante vertical admissivel para que a tensão de cisalhamento na viga não exceda 90 MPa.
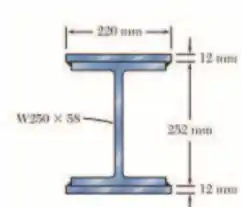
Passo 1
E ai gurizada tudo beleza? O enunciado pede que a gente determinar a maior força cortante vertical admissivel para que a tensão de cisalhamento na viga não exceda 90 MPa.. .... Então partiu!
Começaremos calculando momento de inércia :D , dividindo o elemento em seções, como esboçado abaixo.
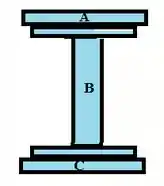
O diâmetro temos:
Calculando a inércia temos:
Sendo a espessura de t= 0,008 m
Passo 2
Considere o esboço abaixo :D
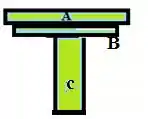
De maneira analoga vamos calcular a inercia :D
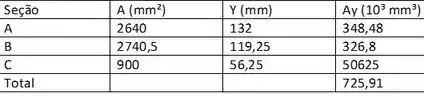
Temos então que:
Para determinarmos a força cortante temos:
Resposta
Exercícios de Livros Relacionados
A viga de seção composta mostrada foi fabricada conectando dois perfis laminados W150x29,8 por meio de parafusos com 15,88m m ,Sabendo que a tensão de cisalhamento média admissível para os parafusos é
Para a viga e carregamento mostrado, considere a seção n-n e determinar (a) o maior tensão de cisalhamento nessa seção, (b) a tensão de cisalhamento ponto a.
Para uma viga com a seção transversal mostrada, determine a maior cisalhamento vertical permitido se a tensão de cisalhamento não exceder 60 MPa.
Para uma viga de madeira com a seção transversal mostrada, determine a maior força cortante vertical admissivel se a tensão de cisalhamento não deve exceder 150 psi.
Para uma viga com a seção transversal mostrada, determine a maior cisalhamento vertical permitido se a tensão de cisalhamento não exceder 60 MPa.