Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 61
Se a mola BC esta descarregada com e a alavanca excêntrica atinge sua posição de equilíbrio quando , determine a força F aplicada perpendicularmente ao segmento AD e as componentes horizontais e verticais da reação no pino A. A mola BC permanece na posição horizontal em todo o tempo devido ao rolete em C
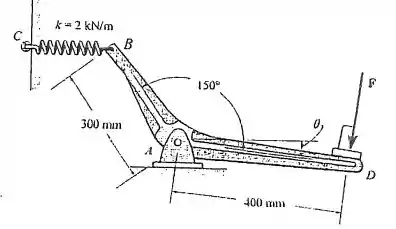
Passo 1
Bem estamos em equilíbrio então As forças verticais, horizontais e Momentos binários se anulam
Vamos dar uma olhada no diagrama de forças
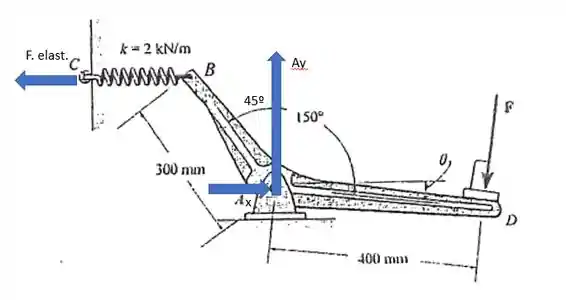
Vamos por partes que essa maquina tem varias peculiaridades. Primeiro, A alavanca é uma peça única. Meio obvio eu sei, mas é importante porque quando aplicamos uma força em D e fazemos a alavanca girar, A parte AB também gira a mesma angulação.
Então Vamos olhar para a parte a mola.
Com a alavanca parada em a mola não faz nenhuma força. O problema nos diz isso. Então se formos considerar o angulo entre AB e o eixo vertical( podemos olhar para Ay , por exemplo ), vamos chamar esse ângulo de temos
Depois que rodamos a alavanca temos que
Então Com a mola tensionada temos Essa diferença de 60 para 45.
Agora F é perpendicular ao braço da alavanca então por isso ele não precisa ser decomposto em componentes verticais e horizontais. Ele já está prontinho !!!
Se ficar na duvida é so lembrar que
Neste caso o seno entre R e F é 1.
Passo 2
Vamos definir uma Orientação antes de começar. Gosto sempre de trabalhar em sentido horário. Essa orientação é arbitrária, se você estiver feito no sentido contrário, beleza! Só ao conferir as contas os sinais estarão trocados.
Então vamos lá. Tudo o que fizer meu sistema tentar rodar em Horario é ( + ), tudo o que tentar fazer tentar rodar em sentido contrario é ( - ) .
Outra coisa. Quando fazemos momento Binário temos que olhar para o PAR distancia e força. Elas têm que ser ortogonais. Show! Vamos cair dentro.
Passo 3
Vamos fazer o momento binário do sistema
Precisamos achar a Força elástica. Bem ....sabemos que o modulo de F. el = kx. Já é um ótimo ponto de partida. E melhor temos k. Então so precisamos achar o X
No inicio descobrimos que antes de F, o braço AB fazia um ângulo com a vertical de 60, e depois de F passou a fazer 45. Então vamos por isso na conta
Achamos \o/. agora vamos jogar de volta no nosso sistema
Agora podemos Achar Ay e Ax. Neste ponto temos que decompor F em Fx e Fy. Lembre estamos trabalhando agora só com força ortogonais.
Então passando tudo para , obtemos que:
Prontinho 😊