Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 18
Determine as componentes horizontal e vertical da reação no pino C e a força na trva do guincho no problema 10
Passo 1
Bem Vamos relembrar que questão é essa?
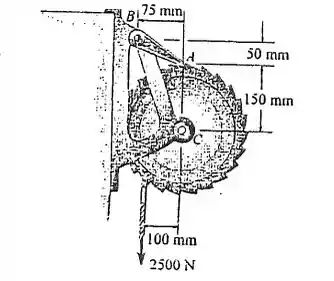
Tinhamos esse tambor Apoiado em C pela peça AB. Fizemos o diagrama de forças
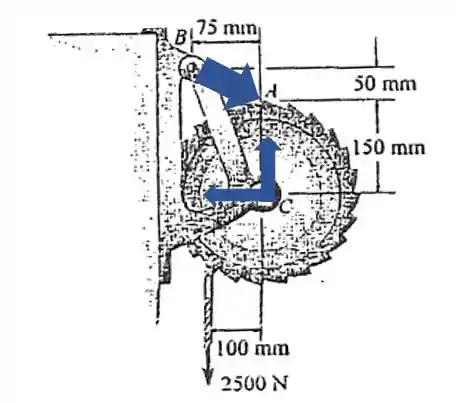
E descobrimos as direções dessas forças. Então antes de ir mais adiante. Vamos decompor força T feito pela trava AB.
Basicamente precisamos de Tsen e Tcos
E como sabemos
Podemos usar Pitagoras para achar a hipotenusa.
Então
E analogamente
Passo 2
Bem estamos em equilíbrio então As forças verticais, horizontais e Momentos binários se anulam
Vamos definir uma Orientação antes de começar. Gosto sempre de trabalhar em sentido horário. Essa orientação é arbitrária, se você estiver feito no sentido contrário, beleza! Só ao conferir as contas os sinais estarão trocados.
Então vamos lá. Tudo o que fizer meu sistema tentar rodar em Horario é ( + ), tudo o que tentar fazer tentar rodar em sentido contrario é ( - ) .
Outra coisa. Quando fazemos momento Binário temos que olhar para o PAR distancia e força. Elas têm que ser ortogonais. Show! Vamos cair dentro.
Passo 3
Vamos fazer o momento binário do sistema.
Só lembra que queremos distancias ortogonais. Então quando formos levar em consideração as forças verticais, precisamos pegar a projeção horizontal da parte inclinada ; )
Prontinho 😊