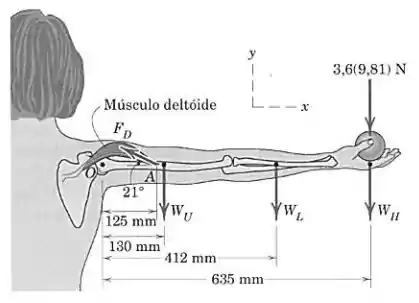
Uma mulher está segurando uma esfera de em sua mão, mantendo todo seu braço na horizontal, como mostrado na figura. Uma força trativa no músculo deltoide impede o braço de girar em torno do ombro ; essa força atua no ângulo de mostrado. Determine a força exercida pelo músculo deltoide no braço, em , e as componentes e da força de reação no ombro, em . A massa do braço é , a massa do antebraço é e a massa da mão é ; com os pesos correspondentes atuando nas posições mostradas na figura.

Através da equação de equilíbrio de forças na horizontal, podemos calcular a componente da força em :

Agora, usando a equação de equilíbrio de forças na vertical, calculamos a componente da força em :