Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas Revisão - Ex. 140

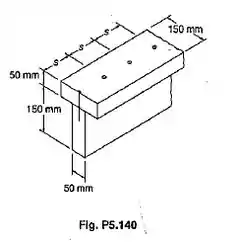
Duas pranchas de 50 x 150 mm de seção transversaç são conectadas através de parafusos de fenda, para formar uma viga que é submetida a uma força vertical de 1800 N. Sabendo-se que a força de cisalhamento admissível é de 1600 N em cada parafuso, determinar: (a) o maior espaçamento longitudinal permissível para os parafusos de fenda; (b) a correspondente tensão de cisalhamento máxima na viga.

Passo 1

Para resolvermos essa questão, precisamos antes de mais nada separar o perfil em áreas diferentes. Fiamos do seguinte jeito

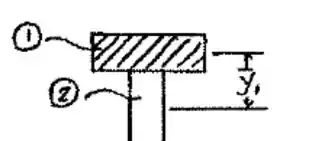
Vamos começar calculando a posição do y - . Para isso fazemos

y - = 150 50 175 + 150 50 75 2 ( 150 × 50 ) = 125   m m

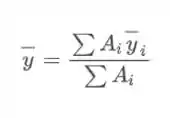
Calculando o momento de inércia da região 1

I 1 = 1 12 b h 3 + A d 2 = 1 12 150 50 3 + 150 50 50 2 = 20,31 × 10 6 m m 4

I 2 = 1 12 b h 3 + A d 2 = 1 12 50 150 3 + 150 50 50 2 = 32,81 × 10 6   m m 4

Nosso I total será dado pela soma desses resultados

I = I 1 + I 2 = 53,12 × 10 6 m m 4

Para o calculo de Q temos

Q = A 1 y 1 - = 150 50 50 = 375 × 10 3 m m 3

Passo 2

Para resolvermos essa questão temos a relação

q s = F   e   q = V Q I

Onde s é o espaçamento entre os pregos. Juntando então as fórmulas e isolando s.

s = F I V Q = 1600   53,12 × 10 6 1800 375 × 10 3 = 125,9   m m

Resposta

s = 125,9   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga extrudada tem seção transversal como mostrado e uma espessura de parede constante e igual a 3 m m . Para uma força cortante vertical de 10 k N , determinar:A tensão de cisalhamento no ponto A
Uma viga extrudada tem seção transversal como mostrado e uma espessura de parede constante e igual a 3 m m . Para uma força cortante vertical de 10 k N , determinar:A máxima tensão de cisalhamento na
Uma viga com a seção transversal mostrada é submetida a uma força cortante vertical V . Determine (a) a linha horizontal ao longo da qual a tensão de cisalhamento máxima. (b) a constante k na expressã
A viga fabricada mostrada é feita colando duas tiras de madeira compensada de 20 x 250 mm e duas pranchas de 50 x 100 mm. Sabendo que a tensão de cisalhamento média nas juntas coladas é de 350 kPa, de
Uma placa de 2 mm de espessura é dobrada conforme mostrado, e então usada como viga. Para uma força cortante vertical de 5 kN, determine a tensão de cisalhamento nos cinco pontos indicados e esquemati