Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 30
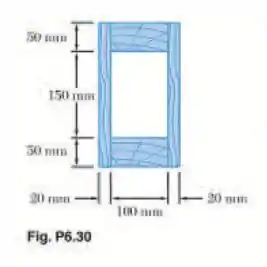
A viga fabricada mostrada é feita colando duas tiras de madeira compensada de 20 x 250 mm e duas pranchas de 50 x 100 mm. Sabendo que a tensão de cisalhamento média nas juntas coladas é de 350 kPa, determine a maior força cortante vertical permitida na viga.
Passo 1
Beleza! Para encontrar a maior força cortante vertical permitida na viga, vamos utilizar a equação para a tensão de cisalhamento, dada por:
Em que V é a força cortante, Q é o momento de área, I é o momento de inércia e t é a espessura da seção. Então, precisamos encontrar os valores do momento de inércia e do momento de área, pois a tensão de cisalhamento foi dada no enunciado e a espessura conseguimos encontrar através da figura.
Passo 2
Tá legal! Vamos começar encontrando o momento de inércia para a seção. No nosso caso, como temos uma seção vazada, vamos encontrar o momento de inércia pegando a área total e subtraindo a área interna vazada. Dessa forma, teremos:
Substituindo os valores conhecidos, temos:
Agora, para encontrar o momento de área, não podemos esquecer que estamos interessados na força de cisalhamento vertical das juntas coladas, então, nossa área de interesse será somente a área destacada a seguir:
Observe que já destacamos a distância entre o centroide da nossa seção de interesse e o centroide da seção como um todo. Agora então podemos calcular o momento de área, dado por:
Substituindo os valores conhecidos, teremos:
Passo 3
Certo! Agora precisamos da espessura da área de interesse, no nosso caso, são 50 mm em cada um dos lados da junta, então, a espessura total de contato será:
Agora podemos utilizar a equação da tensão de cisalhamento, dada por:
E isolar a força cortante, chegando em:
E, substituindo os valores conhecidos, chegamos em:
E essa é a maior força cortante vertical permitida para as condições dadas.