Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 32
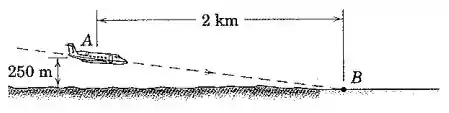
Durante a sua aproximação final da pista, a velocidade da aeronave é reduzida de em para em . Determine a força aerodinâmica externa que age sobre a aeronave de durante esse intervalo, e encontre as componentes dessa força que são paralelas e normais à trajetória de voo.
Passo 1
Galera, o pulo do gato aqui é perceber que a gente pode olhar o problema como se o avião estivesse descendo um grande plano inclinado, cuja inclinação é:
Considerando a direção como paralela à trajetória de voo (reta pontilhada), vão atuar aí uma componente do peso do avião e uma componente da força aerodinâmica, contrária à . Pela Segunda Lei de Newton:
Passo 2
Para conhecer a aceleração , usamos a seguinte equação:
Então podemos substituir todos os valores na expressão de :
Passo 3
Voltando à analogia com o plano inclinado, a trajetória do avião segue uma linha reta, o que significa que as forças perpendiculares a essa linha se equilibram. No caso, essas forças são a componente do peso e a componente da força aerodinâmica, que faria aqui um papel tipo a força normal do plano inclinado. Então escrevemos:
Portanto, o módulo de vai ser dado por:
Resposta
(paralela à trajetória)
(normal à trajetória)